(本题满分13分)已知函数 .
.
(Ⅰ) 求函数 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)已知 内角
内角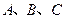 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值.
 北京期货商会组织结构设置如下:
北京期货商会组织结构设置如下:
(1)会员代表大会下设监事会、会长办公会,而会员代表大会于会长办公会共辖理事会;
(2)会长办公会设会长,会长管理秘书长;
(3)秘书长具体分管:秘书处、规范自律委员会、服务推广委员会、发展创新 委员会。
委员会。
根据以上信息绘制组织结构图。
在复平面内,点P、Q所对应的复数分别为z1、z2,且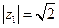 ,
, ,求点Q的集合表示的图形.
,求点Q的集合表示的图形.
(12分 )已知集合A={x|x
)已知集合A={x|x 2-3x+2=0}
2-3x+2=0} ,B={x|x2-ax+3a-5=0},若A∩B=B,
,B={x|x2-ax+3a-5=0},若A∩B=B,
求实数a的值.
 若
若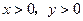 且
且 ,求证:
,求证: 或
或 中至少有一个成立.
中至少有一个成立.
(本题14分)已知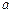 为实数,函数
为实数,函数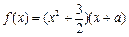 .
.
(I)若函数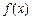 的图象上有与
的图象上有与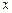 轴平行的切线,求
轴平行的切线,求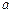 的取值范围;
的取值范围;
(II)若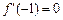 ,
,
(ⅰ) 求函数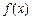 的单调区间;
的单调区间;
(ⅱ) 证明对任意的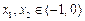 ,不等式
,不等式 恒成立。
恒成立。