(本小题满分12分)
已知向量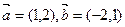 ,
,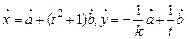 ,k,t为实数.
,k,t为实数.
(Ⅰ)当k=-2时,求使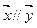 成立的实数t值;
成立的实数t值;
(Ⅱ)若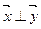 ,求k的取值范围.
,求k的取值范围.
(本题满分12分 )
)
已知圆C: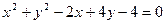 . (1)写出圆C的标准方程;(2)是否存在斜率为1的直线m,使m被圆C截得的弦为AB,且以AB为直径的圆过原点.若存在,求出直线m的方程; 若不存在,说明理由.
. (1)写出圆C的标准方程;(2)是否存在斜率为1的直线m,使m被圆C截得的弦为AB,且以AB为直径的圆过原点.若存在,求出直线m的方程; 若不存在,说明理由.
已知直三棱柱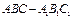 中,
中,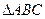 为等腰直角三角形,
为等腰直角三角形, ,且
,且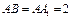 ,D,E,F分别为
,D,E,F分别为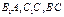 的中点,
的中点,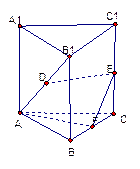
(1)求证: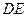 //平面
//平面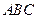 ;
;
(2)求证: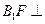 平面
平面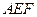 ;
;
(3)求点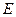 到平面
到平面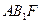 的距离。
的距离。
如图,在底面是直角梯形的四棱锥S-A BCD中,
BCD中,
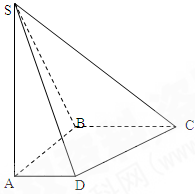
(1)求四棱锥S-ABCD的体积;
(2)求证: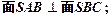
已知关于x,y的方程C: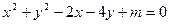 .
.
(1)当m为何值时,方程C表示圆。
(2)若圆C与直线l :x+2y-4=0相交于M,N两点,且
:x+2y-4=0相交于M,N两点,且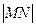 =
= ,求m的值。
,求m的值。
已知:四边形ABCD是空间四边形,E, H分别是边AB,AD的中点,F, G分别 是边CB,CD上的点,且
是边CB,CD上的点,且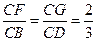 .
.
求证:(1)四边形EFGH是梯形;
(2)FE和GH的交点在直线AC上.