甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是 ,甲、乙、丙三人都能通过测试的概率是
,甲、乙、丙三人都能通过测试的概率是 ,甲、乙、丙三人都不能通过测试的概率是
,甲、乙、丙三人都不能通过测试的概率是 ,且乙通过测试的概率比丙大.
,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;
(Ⅱ)求测试结束后通过的人数 的数学期望
的数学期望 .
.
已知数列 的前
的前 项和为
项和为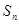 ,且满足
,且满足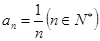 ,若不等
,若不等 对于
对于 恒成立,则自然数
恒成立,则自然数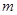 的最大值为
的最大值为
已知 ,且满足
,且满足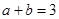 ,则
,则 的最小值为
的最小值为
(本小题14分)已知单调递增的等比数列{an}满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn= ,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
,Sn=b1+b2+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算?
已知数列{an}的前n项和是Sn,且Sn+ an=1.
an=1.
(1)求数列{an}的通项公式;
(2)设bn=log3(1-Sn+1),求适合方程 +
+ +…+
+…+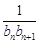 =
=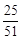 的n的值.
的n的值.