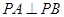函数 满足:①定义域是
满足:①定义域是 ; ②当
; ②当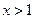 时,
时,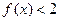 ;
;
③对任意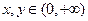 ,总有
,总有
(1)求出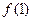 的值;
的值;
(2)判断函数 的单调性,并用单调性的定义证明你的结论;
的单调性,并用单调性的定义证明你的结论;
(3)写出一个满足上述条件的具体函数。
设曲线 在点
在点 处的切线与y轴交于点
处的切线与y轴交于点 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求
,求 .
.
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为 平方米.
平方米.
(1)分别写出用 表示
表示 和用
和用 表示
表示 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
如图,在正三棱柱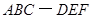 中,
中, 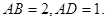
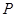 是
是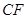 的沿长线上一点,
的沿长线上一点,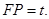 过
过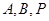 三点的平面交
三点的平面交 于
于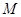 ,交
,交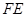 于
于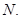
(Ⅰ)求证: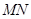 ∥平面
∥平面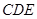 ;
;
(Ⅱ)当平面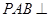 平面
平面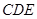 时,求
时,求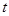 的值.
的值.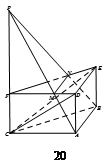
已知 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为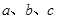 ,向量
,向量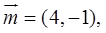
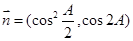 ,且
,且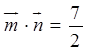 .
.
Ⅰ)求角A的大小;
Ⅱ)若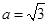 ,试判断
,试判断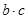 取得最大值时
取得最大值时 形状
形状
已知椭圆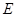 :
: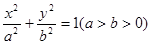 的左焦点
的左焦点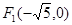 ,若椭圆上存在一点
,若椭圆上存在一点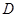 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段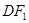 相切于线段
相切于线段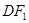 的中点
的中点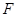 .
.
(Ⅰ)求椭圆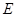 的方程;
的方程;
(Ⅱ)已知两点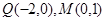 及椭圆
及椭圆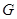 :
: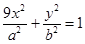 ,过点
,过点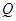 作斜率为
作斜率为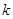 的直线
的直线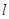 交椭圆
交椭圆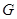 于
于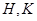 两点,设线段
两点,设线段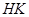 的中点为
的中点为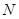 ,连结
,连结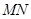 ,试问当
,试问当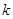 为何值时,直线
为何值时,直线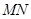 过椭圆
过椭圆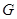 的顶点?
的顶点?
(Ⅲ) 过坐标原点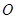 的直线交椭圆
的直线交椭圆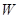 :
: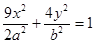 于
于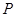 、
、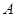 两点,其中
两点,其中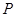 在第一象限,过
在第一象限,过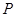 作
作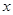 轴的垂线,垂足为
轴的垂线,垂足为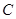 ,连结
,连结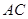 并延长交椭圆
并延长交椭圆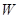 于
于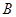 ,求证:
,求证: