一辆汽车沿着一条南北方向的公路来回行驶。某一天早晨从A地出发,晚上到达B地。
约定向北为正,向南为负,当天记录如下:(单位:千米)
-18.3, -9.5, +7.1, -14, -6.2, +13, -6.8, -8.5
(1)问B地在A地何处,相距多少千米?
(2)若汽车行驶每千米耗油0.2升,那么这一天共耗油多少升?
(1)如图1,若D、E分别是△ABC的边AB、AC上的中点,我们把这样的线段DE称为是三角形的中位线.你知道中位线DE与BC之间有什么关系吗?请同学们大胆地猜想一下,并证明你的结论.
(2)如示意图2,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离(精确到1m).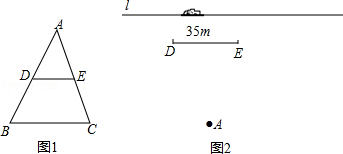
(1)如图所示,如果你的位置在点A,你能看到后面那座高大的建筑物吗?为什么?
(2)如果两楼之间相距MN=20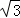 m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?此时,你的视角α是多少度?
m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?此时,你的视角α是多少度?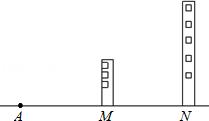
如图,小华家(点A处)和公路(l)之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线.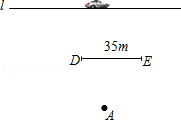
(1)请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.
(2)一辆匀速行驶的汽车经过公路BC段的时间是3s,已知广告牌和公路的距离是40m,小华家到广告牌的距离为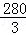 m,求汽车匀速行驶的速度.
m,求汽车匀速行驶的速度.
如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.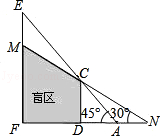
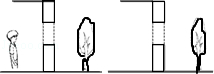
小明同学在教室透过窗户看外面的小树,他能看见小树的全部吗?请在图1中画说明.如果他想看清楚小树的全部,应该往(填前或后)走.在图2中画出视点A(小明眼睛)的位置.