小明做了四个正方形或长方形纸板如图1所示a、b为各边的长,小明用这四个纸板拼成图2图形,验证了完全平方公式。小明说他还能用这四个纸板通过拼接、遮盖,组成新的图形,来验证平方差公式.他说的是否有道理?如有道理,请你帮他画出拼成的图形.如没有道理、不能验证,请说明理由.并与同伴交流.

图1 (a+b)2=a2+2ab+b2
图2
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.
如图,有四张背面相同的纸牌A,B,C,D,其正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色.小明将这4张纸牌背面朝上洗匀后,摸出一张,将剩余3张洗匀后再摸出一张.请用画树状图或列表的方法求摸出的两张牌均为黑色的概率.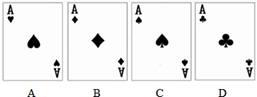
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,求EC的长.
画图:
(1)如图,已知△ABC和点O.将△ABC绕点O顺时针旋转90°得到△A1B1C1,在网格中画出△A1B1C1;
(2)如图,AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺(只能画线)按要求画图.
(ⅰ)在图1中,画出△ABC的三条高的交点;
(ⅱ)在图2中,画出△ABC中AB边上的高.