画图：
（1）如图，已知△ABC和点O．将△ABC绕点O顺时针旋转90°得到△A1B1C1，在网格中画出△A1B1C1；
（2）如图，AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺（只能画线）按要求画图．
（ⅰ）在图1中，画出△ABC的三条高的交点；
（ⅱ）在图2中，画出△ABC中AB边上的高．
如图，在10×10的正方形网格中，每个小正方形的边长均为1个单位．
（1）作△ABC关于点P的对称图形△A′B′C′；
（2）再把△A′B′C′，绕着C'逆时针旋转90°，得到△A″B″C′，请你画出△A′B′C′和△A″B″C′．（不要求写画法）
如下图所示，已知△ABC内接于⊙O，BD为直径，AB=AC，
.
(1)求证：△ABC为等边三角形；
（2）求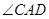
的度数.
观察下列各式：
； 
； 
……，
请你猜想：
(1) 
，
。
(2) 计算(请写出推导过程)：
(3) 请你将猜想到的规律用含有自然数n（n≥1）的代数式表达出来，并验证其正确性.
已知
是方程
的一个根，试求
的值。
解方程： （每小题5分，共10分）
（1）2(x+3)2 =x+3．（2）x2 –x+1=0