如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.
(1)作△ABC关于点P的对称图形△A′B′C′;
(2)再把△A′B′C′,绕着C'逆时针旋转90°,得到△A″B″C′,请你画出△A′B′C′和△A″B″C′.(不要求写画法)
如图,已知在直角梯形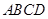 中,
中,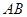 ∥
∥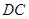 ,
,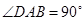 ,AD=DC=
,AD=DC=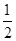 AB,E是AB的中点。
AB,E是AB的中点。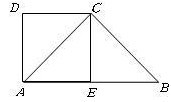
求证:四边形AECD是正方形
求∠B的度数
如图,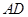 是
是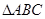 的一条角平分线,
的一条角平分线,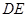 ∥
∥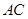 交
交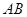 于点
于点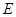 ,
,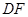 ∥
∥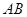 交
交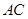 于点
于点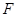 ,求证:四边形
,求证:四边形 是菱形
是菱形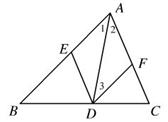
证明:
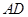 是
是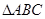 的一条角平分线
的一条角平分线
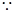
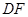 ∥
∥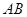
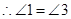 ()
()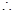 ____________(等量代换)
____________(等量代换)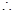 ____________(等角对等边)
____________(等角对等边)
又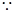
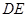 ∥
∥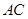 ,
,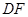 ∥
∥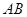
即___________________,_____________________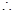 四边形
四边形 是平行四边形(_________________________________)
是平行四边形(_________________________________)
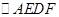 是菱形(____________________________________________)
是菱形(____________________________________________)
甲、乙两同学玩“托球赛跑”游戏,商定,用球拍托着乒乓球从起跑线L起跑,绕过P点跑回起跑线,如图所示,途中乒乓球掉下时需捡起并回到掉球处继续赛跑,用时少者获胜。结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完。事后,甲同学说:“我俩所用的全部时间为50秒”。乙同学说:“捡球过程不算在内时,甲的速度是我的1.2倍”。根据图文信息,请问哪位同学获胜?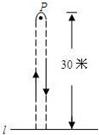
如图,正比例函数y=ax的图象与反比例函数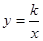 的图象交于点A(-3,2)。
的图象交于点A(-3,2)。
确定上述正比例函数和反比例函数的解析式
根据图象回答:在第二象限内,当x取何值时,反比例函数的值大于正比例函数的值?
M(m,n)是反比例函数图象上的一动点,其中-3<m<0,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D,当四边形DAOM的面积为6时,请判断线段MB与MD的大小关系,请说明理由。
眉山市三苏公园计划在健身区铺设广场砖。现有甲、乙两个工程队参加竞标,甲工程队铺设广场砖的造价y甲(元)与铺设面积x(㎡)的函数关系如下图所示;乙工程队铺设广场砖的造价y乙(元)与铺设面积x(㎡)的函数关系式y乙=kx。
根据图示写出甲工程队铺设广场砖的造价y甲(元)与铺设面积x(㎡)的函数关系式,并注明自变量的取值范围。
若三苏公园铺设广场砖的面积为1600㎡,则当k为何值时,公园选择乙工程队施工更合算?