已知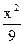 +
+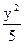 =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
求圆 关于原点对称的圆的方程,并求这两个圆的外公切线方程.
关于原点对称的圆的方程,并求这两个圆的外公切线方程.
如图,已知四边形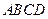 是等腰梯形,
是等腰梯形, 、
、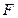 分别是腰
分别是腰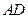 、
、 的中点,
的中点,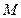 、
、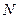 是线段
是线段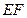 上的两个点,且
上的两个点,且 ,下底是上底的2倍,若
,下底是上底的2倍,若 ,
,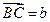 ,求
,求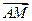 .
.

在一家保险公司的董事会上,董事们就我国加入世界贸易组织(WTO)后公司的发展战略问题展开激烈讨论,其中一个议题是如何借鉴国外保险公司先进的管理经验,改进公司的管理模式.会议决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.这个销售目标确定的是否合适,直接影响公司的经济效益.如果目标过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元):
请根据这组样本数据提出使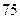 %的职工能够完成销售指标的建议.
%的职工能够完成销售指标的建议.
已知向量 ,
, ,
,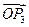 满足条件
满足条件 ,
, ,求证
,求证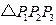 是正三角形.
是正三角形.
如图, ,
,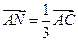 .求证:
.求证: .
.
