某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
已知圆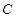 :
:
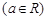 ,过定点
,过定点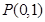 作斜率为1的直线交圆
作斜率为1的直线交圆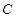 于
于 、
、 两点,
两点,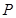 为线段
为线段 的中点.
的中点.
(1)求 的值;
的值;
(2)设 为圆
为圆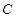 上异于
上异于 、
、 的一点,求△
的一点,求△ 面积的最大值;
面积的最大值;
(3)从圆外一点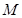 向圆
向圆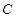 引一条切线,切点为
引一条切线,切点为 ,且有
,且有 , 求
, 求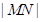 的最小值,并求
的最小值,并求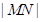 取最小值时点
取最小值时点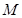 的坐标.
的坐标.
圆 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦.
的弦.
(1)当 时,求
时,求 ;
;
(2)当弦 被点
被点 平分时,求出直线
平分时,求出直线 的方程;
的方程;
(3)设过 点的弦的中点为
点的弦的中点为 ,求点
,求点 的坐标所满足的关系式.
的坐标所满足的关系式.
已知△ 中,
中, ,
, ,
, 平面
平面 ,
, ,
, 、
、 分别是
分别是 、
、 上的动点,且
上的动点,且
 .
.
(1)求证:不论 为何值,总有平面
为何值,总有平面 平面
平面 ;
;
(2)当 为何值时,平面
为何值时,平面 平面
平面 ?
?
已知多面体 中, 四边形
中, 四边形 为矩形,
为矩形, ,
, ,平面
,平面 平面
平面 ,
,  、
、 分别为
分别为 、
、 的中点,且
的中点,且 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)设平面 将几何体
将几何体 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为 ,
, ,求
,求 的值.
的值.
已知函数 .
.
(1)若 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;
(2)当 时,若对任意的
时,若对任意的 ,总存在
,总存在 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.