已知圆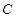 :
:
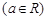 ,过定点
,过定点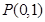 作斜率为1的直线交圆
作斜率为1的直线交圆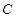 于
于 、
、 两点,
两点,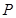 为线段
为线段 的中点.
的中点.
(1)求 的值;
的值;
(2)设 为圆
为圆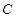 上异于
上异于 、
、 的一点,求△
的一点,求△ 面积的最大值;
面积的最大值;
(3)从圆外一点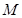 向圆
向圆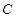 引一条切线,切点为
引一条切线,切点为 ,且有
,且有 , 求
, 求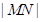 的最小值,并求
的最小值,并求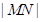 取最小值时点
取最小值时点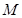 的坐标.
的坐标.
已知四棱锥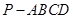 中,
中,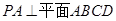 ,底面
,底面 是边长为
是边长为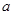 的菱形,
的菱形,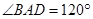 ,
, .
.
(I)求证: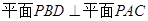 ;
;
(II)设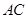 与
与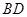 交于点
交于点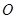 ,
,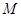 为
为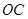 中点,若二面角
中点,若二面角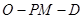 的正切值为
的正切值为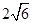 ,求
,求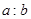 的值.
的值.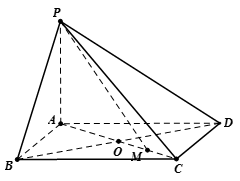
在数列 中,
中,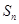 为其前
为其前 项和,满足
项和,满足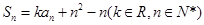 .(I)若
.(I)若 ,求数列
,求数列 的通项公式;
的通项公式;
(II)若数列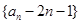 为公比不为1的等比数列,求
为公比不为1的等比数列,求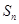 .
.
已知 ,满足
,满足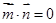 .
.
(I)将 表示为
表示为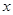 的函数
的函数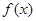 ,并求
,并求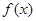 的最小正周期;
的最小正周期;
(II)已知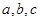 分别为
分别为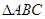 的三个内角
的三个内角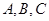 对应的边长,若
对应的边长,若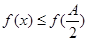 对所有
对所有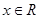 恒成立,且
恒成立,且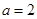 ,求
,求 的取值范围.
的取值范围.
(本题192班必做题,其他班不做)
已知二次函数f(x)=ax2+bx+c,若f(x)+f(x+1)=2x2-2x+13
(1)求函数f(x)的解析式;
(2)画该函数的图象;
(3)当x∈[t,5]时,求函数f(x)的最大值.
(本题192班不做,其他班必做)
已知二次函数f(x)满足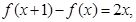 且f(0)=1.
且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)在区间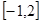 上求y= f(x)的值域。
上求y= f(x)的值域。