某地政府为科技兴市,欲在如图所示的矩形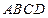 的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形
的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形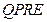 (线段
(线段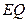 和
和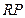 为两个底边),已知
为两个底边),已知
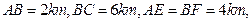 其中曲线段
其中曲线段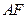 是以
是以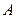 为顶点、
为顶点、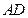 为对称轴的抛物线的一部分.分别以直线
为对称轴的抛物线的一部分.分别以直线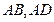 为
为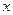 轴和
轴和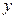 轴建立平面直角坐标系.(1)求曲线段
轴建立平面直角坐标系.(1)求曲线段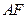 所在抛物线的方程;(2)设点
所在抛物线的方程;(2)设点 的横坐标为
的横坐标为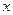 ,高科技工业园区的面积为
,高科技工业园区的面积为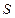 .试求
.试求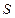 关于
关于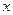 的函数表达式,并求出工业园区面积
的函数表达式,并求出工业园区面积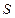 的最大值.
的最大值.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B,E,F,C四点共圆.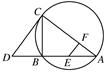
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值.
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D,弦AD和BC交于点Q,割线PEF经过点Q交圆O于点E,F,点M在EF上,且∠BAD=∠BMF.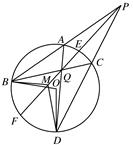
(1)求证:PA·PB=PM·PQ;
(2)求证:∠BMD=∠BOD.
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明: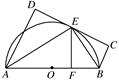
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
如图,圆O的半径OC垂直于直径AB,弦CD交半径 OA于E,过D的切线与BA的延长线交于M.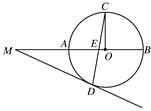
(1)求证:MD=ME;
(2)设圆O的半径为1,MD=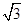 ,求MA及CE的长.
,求MA及CE的长.
如图,已知PE切⊙O于点E,割线PBA交⊙O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
求证:(1)CE=DE;(2)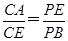 .
.