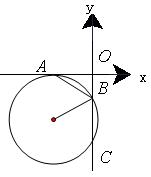
如图,平面直角坐标系中,⊙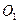 与
与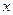 轴相切于点
轴相切于点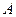 ,与
,与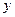 轴相交于点
轴相交于点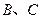 两点,连结
两点,连结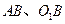 。
。
(1)求证
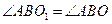 ;
;(2)若点
 的坐标为
的坐标为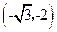 ,直接写出点
,直接写出点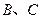 的坐标
的坐标(3)在(2)的条件下,过
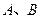 两点作⊙
两点作⊙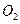 与
与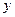 轴的正半轴交于点
轴的正半轴交于点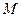 ,与
,与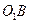 的延长线交于点
的延长线交于点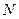 ,当⊙
,当⊙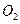 的大小变化时,给出下列两个结论:
的大小变化时,给出下列两个结论: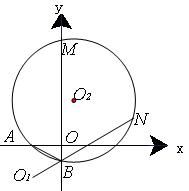
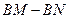 的值不变;②
的值不变;②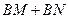 的值不变;
的值不变;
其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值。
如图,在平面直角坐标系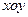 中,抛物线
中,抛物线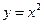 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线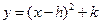 .所得抛物线与
.所得抛物线与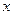 轴交于
轴交于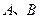 两点(点
两点(点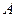 在点
在点 的左边),与
的左边),与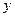 轴交于点
轴交于点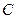 ,顶点为
,顶点为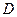 .
.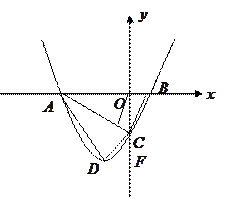
(1)求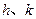 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段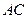 上是否存在点
上是否存在点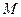 ,使
,使 与
与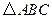 相似.若存在,求出点
相似.若存在,求出点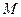 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
有一种螃蟹,从海上捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000 kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10 kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售,并记1000 kg蟹的销售总额为Q元,写出Q关于x的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=Q-收购总额)?
“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.
(1)写出转动一次转盘获得45元购书券的概率;
(2)转转盘和直接获得购书券,你认为哪种方式对读者更合算?请说明理由.
解方程:
(1) 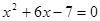 .
.
(2) 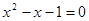
已知 是
是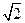 的小数部分,求
的小数部分,求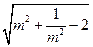 的值
的值