如图所示，两个四分之一圆弧形的光滑轨道AB、CD和粗糙水平轨道BC之间光滑连接。AB弧的半径为R，CD弧的半径为0.7R。BC间距离为3R。质量为m的滑块P（可视为质点）从AB弧的上端从静止释放，第一次通过C点后恰好能到达CD弧的最高点D。重力加速度为g。求：
滑块与水平轨道BC间的动摩擦因数
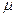；从释放到停止运动滑块在水平轨道BC上滑动的总路程s；
滑块P第一次到达两圆弧最下端的B点和C点时对圆弧轨道的压力大小之比NB：NC。
如图所示,AB为竖直墙壁，A点和P点在同一水平面上。空间存在着竖直方向的匀强电场。将一带电小球从P点以速度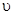
向A抛出，结果打在墙上的C处。若撤去电场，将小球从P点以初速v/2向A抛出，也正好打在墙上的C点。求：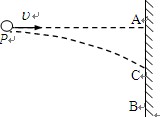
（1）第一次抛出后小球所受电场力和重力之比
（2）小球两次到达C点时速度之比
在一个点电荷Q的电场中，Ox坐标轴与它的一条电场线重合，坐标轴上A、B两点的坐标分别为2.0m和5.0m。放在A、B两点的试探电荷受到的电场力方向都跟x轴的正方向相同，电场力的大小跟试探电荷所带电量的关系图象如图中直线a，b所示，放在A点的电荷带正电，放在B点的电荷带负电。
求：（1）B点的电场强度的大小和方向。
（2）试判断点电荷Q的电性，并说明理由。
（3）点电荷Q的位置坐标。
如图图(甲)所示,A、B是真空中水平放置的一对平行金属板,两板间距离d=15cm。今将B板接地，在A板间加上如图(乙)所示的交变电压(U0 =1080V),然后让一个质量m=1.6×10－27kg、电量大小q=1.6×10-19C的带电粒子(不计重力)在t=0时刻从B板附近由静止开始运动。空气阻力不计。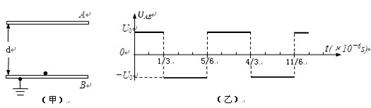
（1）判断粒子的电性；
（2）当t1=?时粒子的速度第一次达到最大，并求出此最大速度；
（3）当粒子的速度第一次达到最大时，粒子的电势能多大？
（4）粒子撞击极板A时的速度为多大？
如图所示的电路中，电源电动势E=24V、内阻r=1Ω,定值电阻R1=15Ω。水平放置的平行金属板AB间距d=40cm,上板A开一小孔。合上电键,适当调整R2的有效阻值，然后让一个质量m=0.02kg、带电量q=-0.01C的小球a从距小孔正上方高h=10cm处自由下落,当a刚进入小孔时,另一小球b(质量、电量与小球a的完全相同)恰好从两板的正中央水平飞入，两球同时打在小孔正下方B板上的P点。小球视为质点，小球间的作用力及空气阻力均忽略不计，g=10m/s2.求：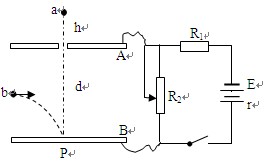
（1）小球a刚进入小孔时的速度V0
（2）两板间的电势差UAB
（3）滑动变阻器的有效阻值
带等量异种电荷的两带电小球A、B，用三根等长的绝缘细线连接后竖直悬挂在一根弹簧上，并置于水平向右的匀强电场中。适当调节电场强度，使三根细线都被拉紧且处于静止状态。若已知细线长为L，两球质量均为m，电量均为q，重力加速度为g，静电力常量为k。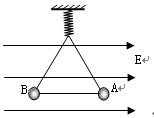
（1）求出满足上述条件的电场强度的最小值Emin
（2）若将电场强度减小到Emin/2，稳定后弹簧的弹力FT =?