在“春季经贸洽谈会”上,我市某服装厂接到生产一批出口服装的订单,要求必须在12天(含12天)内保质保量完成,且当天加工的服装当天立即空运走。为了加快进度,车间采取工人轮流休息,机器满负荷运转的生产方式,生产效率得到了提高。这样每天生产的服装数量y(套)与时间x(元)的关系如下表:
| 时间x(天) |
1 |
2 |
3 |
4 |
… |
| 每天产量y(套) |
22 |
24 |
26 |
28 |
… |
由于机器损耗等原因,当每天生产的服装数达到一定量后,平均每套服装的成本会随着服装产量的增加而增大,这样平均每套服装的成本z(元)与生产时间x(天)的关系如图所示.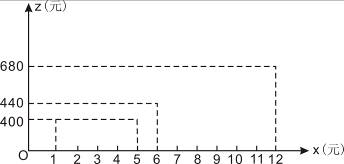
判断每天生产的服装的数量y(套)与生产时间x(元)之间是我们学过的哪种函数关系?并验证.
已知这批外贸服装的订购价格为每套1570元,设车间每天的利润为w(元).求w(元)与x(天)之间的函数关系式,并求出哪一天该生产车间获得最高利润,最高利润是多少元?
从第6天起,该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金,但必须保证每天扣除捐款后的利润随时间的增大而增大.求a的最大值,此时留守儿童共得多少元基金?
如图是一个几何体,请画出它的三视图。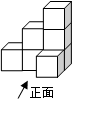
从2开始,连续的偶数相加,它们和的情况如下表:
| 加数的个数n |
S |
| 1 |
2 = 1×2 |
| 2 |
2+4 =" 6" = 2×3 |
| 3 |
2+4+6 =" 12" = 3×4 |
| 4 |
2+4+6+8 =" 20" = 4×5 |
| 5 |
2+4+6+8+10 =" 30" = 5×6 |
(1)若n=8时,则 S的值为_____________.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=____________.
(3)根据上题的规律计算2+4+6+8+10+…+98+100 的值.
的值.
出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:km)如下:-2,+5,-1,+1,-6,-2,问:
(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为0.2L/km(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为3km(包括3km),超过部分每千米1.2元,问小李这天上午共得车费多少元?
列方程解应用题。
把一批图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本。这个班有多少名学生?
若a是绝对值最小的数,b是最大的负整数。先化简,再求值: