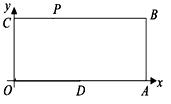
如图1,在平面直角坐标系中有一个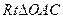 ,点
,点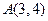 ,点
,点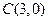 ,将其沿直线AC翻折,翻折后图形为
,将其沿直线AC翻折,翻折后图形为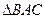 .动点P从点O出发,沿折线
.动点P从点O出发,沿折线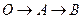 的方向以每秒2个单位的速度向B运动,同时动点Q从点B出发,在线段BO上以每秒1个单位的速度向点O运动,当其中一个点到达终点时,另一点也随之停止运动.设运动的时间为t(秒).
的方向以每秒2个单位的速度向B运动,同时动点Q从点B出发,在线段BO上以每秒1个单位的速度向点O运动,当其中一个点到达终点时,另一点也随之停止运动.设运动的时间为t(秒).设
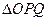 的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围;
的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围;如图2,固定
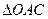 ,将
,将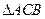 绕点C逆时针旋转,旋转后得到的三角形为
绕点C逆时针旋转,旋转后得到的三角形为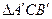 ,设
,设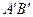 与AC交于点D,当
与AC交于点D,当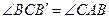 时,求线段CD的长;
时,求线段CD的长;如图3,在
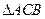 绕点C逆时针旋转的过程中,若设
绕点C逆时针旋转的过程中,若设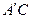 所在直线与OA所在直线的交点为E,是否存在点E使
所在直线与OA所在直线的交点为E,是否存在点E使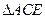 为等腰三角形,若存在,求出点E的坐标,若不存在,请说明理由.
为等腰三角形,若存在,求出点E的坐标,若不存在,请说明理由.
任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE。试说明下列结论正确的理由:(1) ∠C=∠E; (2) AB=AD.
解方程组:
解方程组:
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时,四边形PODB是平行四边形?
(3) 在线段PB上是否存在一点Q,使得ODQP为菱形。若存在求t值,若不存在,说明理由。
(4) 当△OPD为等腰三角形时,求点P的坐标。