观察与发现：
在一次数学课堂上，老师把三角形纸片ABC(AB＞AC)沿过A点的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片(如图①)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF(如图②)．有同学说此时的△AEF是等腰三角形，你同意吗？请说明理由．
实践与运用
将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE(如图③)；再沿过点E的直线折叠，使点D落在BE上的点
处，折痕为EG(如图④)；再展平纸片(如图⑤)．试问：图⑤中∠
的大小是多少？(直接回答，不用说明理由)．
（本 题12分）某种商品的进价为每件50元，售价为每件60元，每个月可卖出200件；如果每件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于72元），设每件商品的售价上涨x元（x为整数），每个月的销售利润为y元。
（1）求y与x的函数关系式并直接写出自变量x的取值范围；
（2）每件商品的售价定为多少时每个月可获得最大利润?最大利润是多少。
（本 题10分）如图，抛物线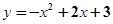
与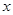
轴分别交于A、B两点。 （1）求点A、B和顶点M的坐标；（2）求△ABM的面积。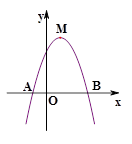
（本 题10分）如图，已知二次函数y=ax2+bx+c的图象经过A（﹣1，﹣1）、B（0，2）、C（1，3）。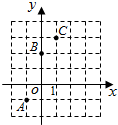
（1）求二次函数的解析式；
（2）画出二次函数的图象；
（本题8分）为了解学区九年级学生对数学知识的掌握情况，在一次数学检测中，从学区2000名九年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：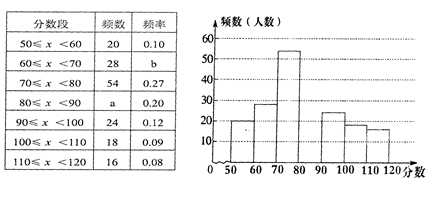
⑴表中a和b所表示的数分别为：a=.，b=.；
⑵请在图中补全频数分布直方图；
⑶如果把成绩在70分以上（含70分）定为合格，那么该学区2000名九年级考生数学成绩为合格的学生约有多少名？
（本题8分）直线y=2x+2与x轴、y轴分别交于A、B两点，将△AOB绕点O顺时针旋转900，得到△A1OB1 。
（1）在图中画出△A1OB1；
（2）求经过A,A1,B1三点的抛物线的解析式。