先阅读,再解答:
我们在判断点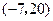 是否在直线
是否在直线 上时,常用的方法:把
上时,常用的方法:把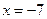 代入
代入 中,由
中,由 ,判断出点
,判断出点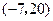 不在直线
不在直线 上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
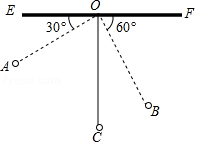
如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在 OA的位置时俯角∠ EOA=30°,在 OB的位置时俯角∠ FOB=60°,若 OC⊥ EF,点 A比点 B高7 cm.求:
(1)单摆的长度( ≈1.7);
(2)从点 A摆动到点 B经过的路径长(π≈3.1).
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.

一汽车从甲地出发开往相距240 km的乙地,出发后第一小时内按原计划的速度匀速行驶,1小时后比原来的速度加快 ,比原计划提前24 min到达乙地,求汽车出发后第1小时内的行驶速度.
在平面直角坐标系 xOy中,抛物线 y= ax 2+ bx+ c与 y轴交于点 C,其顶点记为 M,自变量 x=﹣1和 x=5对应的函数值相等.若点 M在直线 l: y=﹣12 x+16上,点(3,﹣4)在抛物线上.
(1)求该抛物线的解析式;
(2)设 y= ax 2+ bx+ c对称轴右侧 x轴上方的图象上任一点为 P,在 x轴上有一点 A(﹣ ,0),试比较锐角∠ PCO与∠ ACO的大小(不必证明),并写出相应的 P点横坐标 x的取值范围.
(3)直线 l与抛物线另一交点记为 B, Q为线段 BM上一动点(点 Q不与 M重合).设 Q点坐标为( t, n),过 Q作 QH⊥ x轴于点 H,将以点 Q, H, O, C为顶点的四边形的面积 S表示为 t的函数,标出自变量 t的取值范围,并求出 S可能取得的最大值.
如图,点 A, B, C, D是直径为 AB的⊙ O上的四个点, C是劣弧 的中点, AC与 BD交于点 E.
(1)求证: DC 2= CE• AC;
(2)若 AE=2, EC=1,求证:△ AOD是正三角形;
(3)在(2)的条件下,过点 C作⊙ O的切线,交 AB的延长线于点 H,求△ ACH的面积.
