某中学组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
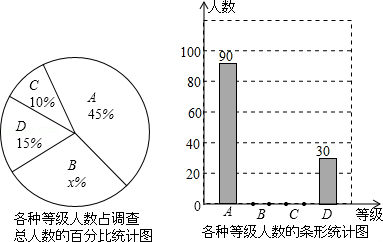
(1)本次随机抽取的学生人数为 人;
(2)求出x值,并将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读量满足2≤t<4的人数.
二次函数y=ax2+bx+c的部分对应值如下表:
| x |
… |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
| y |
… |
5 |
0 |
-3 |
-4 |
-3 |
0 |
… |
(1)二次函数图象所对应的顶点坐标为.
(2)当x=4时,y=.
(3)由二次函数的图象可知,当函数值y<0时,x的取值范围是.
如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).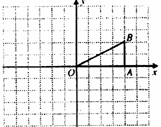
(1)画出△OAB绕点O逆时针旋转90°后的△OA1B1;
(2)求点A旋转到点A1所经过的路线长.
如图,已知CD是Rt△ABC斜边上的高,AC=4,BC=3,计算cos∠BCD的值.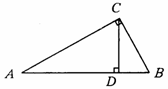
如图,已知⊙O的半径为5,弦AB=8,OC⊥AB于C,求OC的长.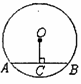
如图,OABC是一个放在平面直角坐标系中的矩形,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=3,OC=4,平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线运动的时间为t(秒).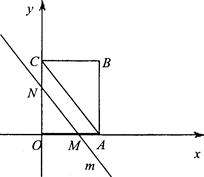
(1)写出点B的坐标;
(2)t为何值时,MN=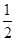 AC;
AC;
(3)设△OMN的面积为S,求S与t的函数关系式,并写出t的取值范围;当t为何值时,S有最大值?并求S的最大值.