如图,梯形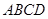 中,
中,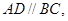 且
且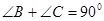 ,
,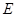 、
、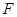 分别是两底的中点,连结
分别是两底的中点,连结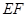 ,若
,若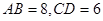 ,求
,求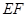 的长。
的长。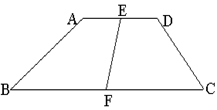
某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考.请你回答下列问题:
| 1号 |
2号 |
3号 |
4号 |
5号 |
总分 |
|
| 甲班 |
100 |
98 |
110 |
89 |
103 |
500 |
| 乙班 |
86 |
100 |
98 |
119 |
97 |
500 |
(1)根据上表提供的数据填写下表:
| 优秀率 |
中位数 |
方差 |
|
| 甲班 |
|||
| 乙班 |
(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级? 简述理由.
工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使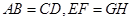 ;
;
(2)摆放成如图②的四边形,则这时窗框的形状是形,根据数学道理是:
;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是形,根据的数学道理是:。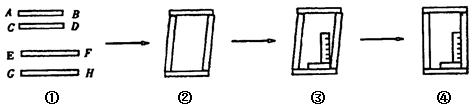
如图,在四边形ABCD中,∠B =90°,AB=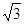 ,∠BAC =30°,CD=2,AD=
,∠BAC =30°,CD=2,AD=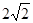 ,求∠ACD的度数。
,求∠ACD的度数。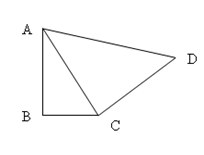
北京时间2010年4月14日7时49分,青海玉树发生7.1级地震,灾情牵动着全国各族人民的心。无为县某中心校组织了捐款活动.小华对八年级(1)(2)班捐款的情况进行了统计,得到如下三条信息:
信息一:(1)班共捐款540元,(2)班共捐款480元.
信息二:(2)班平均每人捐款钱数是(1)班平均每人捐款钱数的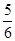 .
.
信息三:(1)班比(2)班少3人.
请你根据以上信息,求出八(1)班平均每人捐款多少元?