(本题6分)探索与思考:
观察下列等式: 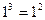
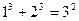
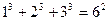
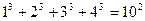
……………………(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?
(2)试一试:13 + 23 + 3 3 + 43 + … + 10 3 = ____________.
(3)猜一猜:可得出什么规律(可用带字母的等式表示,也可用文字表述):
如图,已知反比例函数 (
( )与一次函数
)与一次函数 (
( )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥ 轴于点C,若△OAC的面积为1,且tan∠AOC=2.
轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(1)求反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出当 为何值时,反比例函数
为何值时,反比例函数 的值小于一次函数
的值小于一次函数 的值.
的值.
住在郑东新区的小明知道“中原第一高楼”有多高,他登上了附近的另一座高层酒店的顶层某处.已知小明所处位置距离地面有160米高,测得“中原第一高楼”顶部的仰角为37°,测得“中原第一高楼”底部的俯角为45°,请你用初中数学知识帮小明解决这个问题.(请你画出示意图,并说明理由)(参考数据: )
)
如图1,小颖将一组平行的纸条折叠,点A、B分别落在在A′,B′处,线段FB′与AD交于点M.
(1)试判断△MEF的形状,并证明你的结论;
(2)如图②,将纸条的另一部分CFMD沿MN折叠,点C,D分别落在C′,D′处,且使MD′经过点F,试判断四边形MNFE的形状,并证明你的结论;
(3)当∠BFE=_____度时,四边形MNFE是菱形.
在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.郑州市的一个社区随机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
(1)A组的频数是,本次调查样本的容量是;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
如图,△ABC中,BE、CF分别是∠ABC、∠ACB的角平分线,∠A=50°,那么∠BDC的度数是()
A.105° B.115° C.125° D.135°