用两个全等的正方形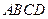
和
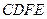拼成一个矩形
，把一个足够大的直角三角尺的直角顶点与这个矩形的边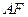
的中点
重合，且将直角三角尺绕点按逆时针方向旋转．
（1）当直角三角尺的两直角边分别与矩形
的两边
相交于点
时，如图甲，通过观察或测量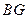
与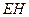
的长度，你能得到什么结论？并证明你的结论．（2）当直角三角尺的两直角边分别与
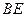的延长线，
的延长线相交于点时（如图乙），你在图甲中得到的结论还成立吗？简要说明理由．
已知：如图，AB为半圆O的直径，C、D是半圆上的两点，E是AB上除O外的一点，AC与DE交于点F．①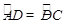
；②DE⊥AB；③AF=DF．请你写出以①、②、③中的任意两个条件，推出第三个（结论）的一个正确命题．并加以证明．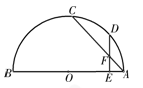
已知：如图，在平面直角坐标系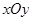
中，直线AB分别与
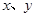轴交于点B、A，与反比例函数的图象分别交于点C、D，
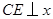轴于点E，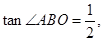
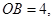
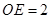．求该反比例函数的解析式．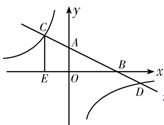
如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处正东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC等于多少米？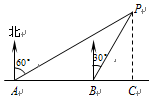
已知:如图,AD平分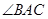
,
,且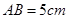
,求DE的长.
在直角坐标系xOy 中，已知某二次函数的图象经过A（－4，0）、B（0，－3），与x轴的正半轴相交于点C，若△AOB∽△BOC（相似比不为1）．（1）求这个二次函数的解析式；
（2）求△ABC的外接圆半径r；
（3）在线段AC上是否存在点M（m，0），使得以线段BM为直径的圆与线段AB交于N点，且以点O、A、N为顶点的三角形是等腰三角形？若存在，求出m的值；若不存在，请说明理由．