如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=14x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.
如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).
(1)求这个二次函数的关系式;
(2)若一次函数y=- x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.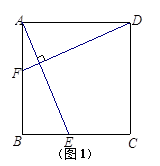
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出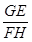 的值.
的值. 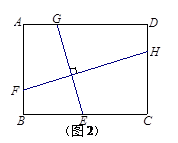
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.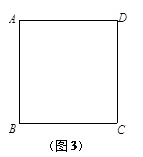
某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=-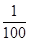 x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳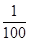 x2元的附加费,月利润为W外(元).
x2元的附加费,月利润为W外(元).
(1)若只在国内销售,当x=1000(件)时,y= (元/件);
(2)分别求出W内、W外与x间的函数关系式(不必写x的取值范围);
(3)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
如图,AB为⊙O的直径,D为⊙O上一点,DE是⊙O的切线,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.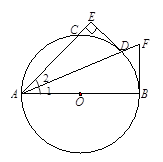
(1)求证:AD平分∠BAC;
(2)若DE=3,⊙O的半径为5,求BF的长.
已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标,并在下面直角坐标系中画出该二次函数的大致图象;
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.