已知二次函数图象的顶点坐标为M(1，0)，直线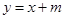
与该二次函数的图象交于A，B两点，其中A点的坐标为(3，4)，B点在
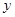轴上．求m的值及这个二次函数的解析式；
若P(
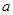，0) 是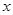
轴上的一个动点，过P作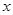轴的垂线分别与直线AB和二次函数的图象交于D、E两点．
①当0<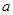< 3时，求线段DE的最大值；
②若直线AB与抛物线的对称轴交点为N，
问是否存在一点P，使以M、N、D、E
为顶点的四边形是平行四边形？若存在，
请求出此时P点的坐标；若不存在，请
说明理由．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠ A的度数．
如图，△ABC是等边三角形，△ADE是等腰三角形，AD=AE，∠DAE=80°，当DE⊥AC时，垂足为F，求∠BAD和∠EDC的度数．
如图，方格纸中每个小正方形的边长均为1，线段AB和PQ的端点均在小正方形的顶点上．
（1）在线段PQ上确定一点C（点C在小正方形的顶点上）．使△ABC是轴对称图形，并在网格中画出△ABC；
（2）请直接写出△ABC的周长和面积．
已知2x－y的平方根为±3，－4是3x＋y的平方根，求x－y的平方根．
解方程（每题4分，共8分）
（1）8x3＋125=0
（2）64（x＋1）2－25=0