(本小题满分14分)如图所示,椭圆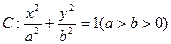 的离心率为
的离心率为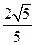 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线 ,设以椭圆C的右焦点F为抛物线
,设以椭圆C的右焦点F为抛物线 的焦点,若点M为抛物线E上任意一点,求点M到直线
的焦点,若点M为抛物线E上任意一点,求点M到直线 距离的最小值。
距离的最小值。
在平面直角坐标系 中,已知抛物线
中,已知抛物线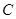 :
: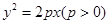 ,在此抛物线上一点
,在此抛物线上一点
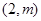 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
(2)抛物线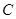 的准线与
的准线与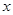 轴交于
轴交于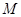 点,过
点,过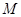 点斜率为
点斜率为 的直线
的直线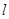 与抛物线
与抛物线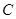 交于
交于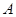 、
、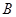 两点.是否存在
两点.是否存在
这样的 ,使得抛物线
,使得抛物线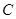 上总存在点
上总存在点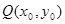 满足
满足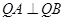 ,若存在,求
,若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本题14分)如图,在三棱锥P—ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC.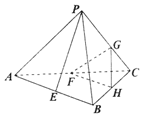
(1)证明:AB⊥PC;(2)证明:PE//平面FGH。
已知命题 :存在
:存在 使得
使得 成立,命题
成立,命题 :对于任意
:对于任意 ,函数
,函数 恒有意义.
恒有意义.
(1)若 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(2)若 是假命题,求实数
是假命题,求实数 的取值范围.
的取值范围.
已知点 是圆
是圆 上任意一点,过点
上任意一点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,点
,点 满足
满足 记点
记点 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设 ,点
,点 在曲线
在曲线 上,且直线
上,且直线 与直线
与直线 的斜率之积为
的斜率之积为 ,求
,求 的面积的最大值.
的面积的最大值.
如图,矩形 所在的半平面和直角梯形
所在的半平面和直角梯形 所在的半平面成
所在的半平面成 的二面角,
的二面角, ∥
∥ ,
, ,
, ,
, ,
, ,
, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)在线段 上求一点
上求一点 ,使锐二面角
,使锐二面角 的余弦值为
的余弦值为