如图所示，质量mB＝3.5kg的物体B通过一轻弹簧固连在地面上，弹簧的劲度系数k=100N/m．一轻绳一端与物体B连接，绕过无摩擦的两个轻质小定滑轮O1、O2后，另一端与套在光滑直杆顶端的、质量mA＝1.6kg的小球A连接．已知直杆固定，杆长L为0.8m，且与水平面的夹角θ=37°．初始时使小球A静止不动，与A端相连的绳子保持水平，此时绳子中的张力F为45N． 已知A O1=0.5m，绳子不可伸长．现将小球A从静止释放（重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8）。求：
在释放小球A前弹簧的形变量；
若直线C O1与杆垂直，求物体A运动到C点的过程中绳子拉力对物体A所做的功；
求小球A运动到底端D点时的速度．
如图所示为某同学设计的节能运输系统．斜面轨道的倾角为37°，木箱与轨道之间的动摩擦因数μ＝0.25.设计要求：木箱在轨道顶端时，自动装货装置将质量m＝2.8kg的货物装入木箱，木箱载着货物沿轨道无初速滑下，当轻弹簧被压缩至最短时，自动装货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，接着再重复上述过程．若g取10 m/s2，sin37°＝0.6，cos37°＝0.8.求：满足设计要求的木箱质量．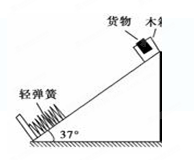
一根长为L、质量不计的硬杆OA，杆的中点C及A端各固定一个质量均为m的小球，杆、球系统可在竖直平面内绕O端的水平轴转动，如图所示.若开始时杆处于水平位置，并由静止释放，当该系统在转动过程中通过竖直位置时，A端小球的速度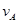
为多大？中点小球的机械能比在水平位置时减少了多少？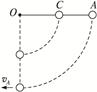
已知地球自转周期T,地球半径为R，地球表面重力加速度为g,请使用上述已知量导出地球同步卫星距离地面的高度h的表达式，并说明同步卫星的轨道特点，运转方向。
如图所示，AB为半径R＝0.8 m的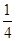
光滑圆弧轨道，下端B恰与小车右端平滑对接。小车质量M＝ 3 kg，车长L＝2.06 m，车上表面距地面的高度h＝0.2 m，现有一质量m＝1 kg的滑块，由轨道顶端无初速释放，滑到B端后冲上小车。已知地面光滑，滑块与小车上表面间的动摩擦因数μ＝0.3，当车运动了1.5 s时，车被地面装置锁定。(g＝10 m/s2)试求：
(1)滑块到达B端时，轨道对它支持力的大小；
(2)车被锁定时，车右端距轨道B端的距离；
(3)从车开始运动到被锁定的过程中，滑块与车面间由于摩擦而产生的内能大小。
如图，质量m=2kg的物体静止于水平地面的A处，A、B间距L=20m。用大小为30N，沿水平方向的外力拉此物体，经t0=2s拉至B处。(sin37º=0.6，cos37º=0.8，g取10m/s2)
(1)求物体与地面间的动摩擦因数μ；
(2)用大小为30N，与水平方向成37°的力斜向上拉此物体，使物体从A处由静止开始运动并能到达B处，求该力作用的最短时间t。（答案可带根号）