(本题满分14分) 设{an}是由正数组成的等差数列,Sn是其前n项和
(1)若 ,求
,求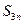 的值;
的值;
(2)若互不相等正整数p,q,m,使得p+q=2m,证明:不等式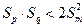 成立;
成立;
(3)是否存在常数k和等差数列{an},使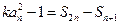 恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
恒成立(n∈N*),若存在,试求出常数k和数列{an}的通项公式;若不存在,请说明理由。
(本小题满分12分)已知数列{an}的首项al=1,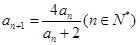 .
.
(1)证明:数列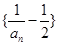 是等比数列;
是等比数列;
(2)设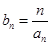 ,求数列
,求数列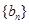 的前n项和
的前n项和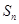 .
.
(本小题满分12分) 已知 、
、 为椭圆的左右焦点,点
为椭圆的左右焦点,点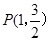 为其上一点,且有
为其上一点,且有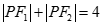
(1)求椭圆的标准方程;
(2)是否存在直线与椭圆交于M,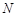 两点,且线段使MN的中点为
两点,且线段使MN的中点为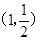 ,若存在,求直线的方程;若不存在,说明理由?
,若存在,求直线的方程;若不存在,说明理由?
(本小题满分12分)已知F1、F2是椭圆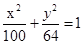 的两个焦点,P是椭圆上任意一点.
的两个焦点,P是椭圆上任意一点.
(1)若∠F1PF2=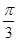 ,求△F1PF2的面积;
,求△F1PF2的面积;
(2)求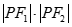 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)已知椭圆 经过点A(0,4),离心率为
经过点A(0,4),离心率为 ;
;
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
(本小题满分12分)已知椭圆 上一点M的纵坐标为2.
上一点M的纵坐标为2.
(1)求M的横坐标;
(2)求过点M且与 共焦点的椭圆方程.
共焦点的椭圆方程.