如图17所示，甲为操作上一质量不计的竖直滑杆，滑杆上端固定，下端悬空，为了研究学生沿杆下滑的情况，在杆的顶部装有一拉力传感器，可显示杆的顶端所受拉力的大小，现有一学生手握滑杆，从杆的上端由静止开始下滑，下滑5s后这个学生的下滑速度为零，并用手紧握住滑杆保持静止不动，以这个学生开始下滑时刻为计时起点，传感器显示的力随时间变化的情况如图乙所示。g=10m/s2，求：
（1）该学生下滑过程中的最大速度；
（2）5s内该学生下滑的距离。
质量为0.5kg的小球从离地高3.75m处以5m/s的水平速度抛出，不计空气阻力，求：（g=l0
）
（1）小球落地时的速度大小。
（2）小球落地点到抛出点的水平距离。
如图一辆质量为500kg的汽车静止在一座半径为50m的圆弧形拱桥顶部则（取g＝10m/s2）：
（1）汽车以多大速度通过拱桥的顶部时，汽车对圆弧形拱桥的压力恰好为零？
（2）如果汽车以6m/s的速度经过拱桥的顶部，则汽车对圆弧形拱桥的压力是多大？
知万有引力常量C，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期Tl，地球的自转周期T2，地球表面的重力加速度g．某同学根据以上条件，提出一种估算地球质量"的方法：
同步卫星绕地心做圆周运动，由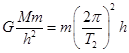
得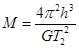
(1)请判断上面的结果是否正确，并说明理由．如不正确，请给出正确的解法和结果
(2)请根据已知条件再提出两种估算地球质量的方法并解得结果
如图7所示,小球A质量为m，固定在轻细绳L的一端,并随绳一起绕绳的另一端O点在竖直平面内做圆周运动。如果小球经过最高位置时,绳对球的作用力为拉力,拉力大小等于2倍球的重力。求：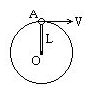
(1)球的速度大小。
(2)当小球经过最低点时速度为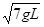
，绳对球的作用力大小和球的向心加速度大小。
把一小球从离地面高h=20m处，以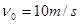
的初速度水平抛出，不计空气阻力， g取10m/s2。求：
(1)小球在空中飞行的时间；
(2)小球落地点离抛出点的水平距离；
(3)小球落地时速度的大小。