(本小题满分12分)如图,在底面是菱形的四棱锥P—ABCD中,∠ABC= ,PA=AC=a,PB=PD=
,PA=AC=a,PB=PD=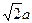 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.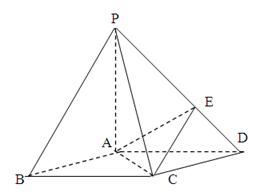
(I)证明PA⊥平面ABCD;
(II)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为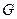 函数。
函数。
①对任意的 ,总有
,总有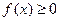 ;
;
②当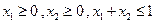 时,总有
时,总有 成立。
成立。
已知函数 与
与 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数 是否为
是否为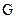 函数?并说明理由;
函数?并说明理由;
(2)若函数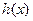 是
是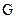 函数,求实数
函数,求实数 的值;
的值;
(3)在(2)的条件下 ,讨论方程
,讨论方程
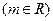 解的个数情况。
解的个数情况。
设数列
满足
,
,
,
。数列
满足
是非零整数,且对任意的正整数
和自然数
,都有
。
(1)求数列
和
的通项公式;
(2)记
,求数列
的前
项和
。
设
,椭圆方程为
,抛物线方程为
.如图所示,过点
作
轴的平行线,与抛物线在第一象限的交点为
,已知抛物线在点
的切线经过椭圆的右焦点
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
,使得
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
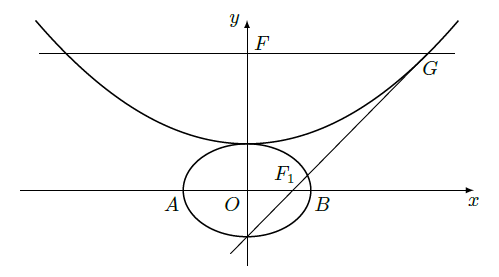
某初级中学共有学生2000名,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知
 245,
245,
 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
如图所示,四棱锥
的底面
是半径为
的圆的内接四边形,其中
是圆的直径,
. 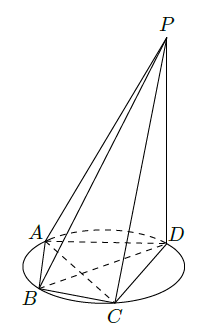
(1)求线段
的长;
(2)若
,求三棱锥
的体积.