某书店的两个下属分店共有某种图书5000册,若将甲书店的该种图书调出400册给乙书店,这样乙书店该种图书的数量仍比甲书店该种图书的数量的一半还少400册.求这两个书店原有该种图书的数量差.
已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线
于C.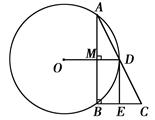
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1, 求⊙O的半径.
求⊙O的半径.
某中学的地理兴趣小组在本校学生中开展主题为“地震知识知多少”的专题调查活
动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基
本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
(1)表中的m的值为_______,n的值为.
(2)根据表中的数据,请你计算“非常了解”的频率在下图中所对应的扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有1500名学生,请根据调查结果估计这些学生中“比较了解”的人数约为多少?
如图,在平行四边形 中,过点A分别作AE⊥BC于点E,AF⊥CD于点
中,过点A分别作AE⊥BC于点E,AF⊥CD于点
F.
(1)求证:∠BAE=∠DAF;
(2)若AE=4,AF= ,
, ,求CF的长.
,求CF的长.
列方程或方程组解应用题
随着人们节能意 识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米.
识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米.
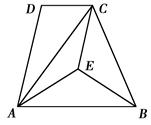
如图,在四边形ABCD中, AC是∠DAE的平分线,DA∥CE,∠AEB="∠CEB."
求证:AB=CB.