让深圳人期待了五年之久的出租车运价调整新方案终于于 年
年 月开始执行,深圳市红色的士调价前后的收费标准对比如下:调整前,起步价
月开始执行,深圳市红色的士调价前后的收费标准对比如下:调整前,起步价 元/
元/ 公里,
公里, 公里后里程价
公里后里程价 元/公里,无返空费;调整后,起步价
元/公里,无返空费;调整后,起步价 元/
元/ 公里,
公里, 公里后里程价
公里后里程价 元/公里,总路程超过
元/公里,总路程超过 公里的,超出部分按里程价的
公里的,超出部分按里程价的 加收返空费.(不考虑红灯等因素)
加收返空费.(不考虑红灯等因素)
(1)小明去 公里外的公园玩,请你估算一下,调价前后乘坐出租车的车费;
公里外的公园玩,请你估算一下,调价前后乘坐出租车的车费;
(2)网上流传“ 公里换车”规避返空费的方法:即乘客的行程超过
公里换车”规避返空费的方法:即乘客的行程超过 公里,就在
公里,就在 公里处下车,换乘另一辆出租车.以下为行程为
公里处下车,换乘另一辆出租车.以下为行程为 、
、 公里换与不换的方法:
公里换与不换的方法:
①若行程为 公里:不换车,总费用为:
公里:不换车,总费用为: 元;
元;
换车,总费用为: 元,因此,行程
元,因此,行程 公里若换车,则费用反而增加
公里若换车,则费用反而增加 元.所以,行程为
元.所以,行程为 公里不换车.
公里不换车.
②若行程为 公里:不换车,总费用为:
公里:不换车,总费用为: 元,若换车,总费用为:
元,若换车,总费用为: 元,则可节约
元,则可节约 元.所以,行程为
元.所以,行程为 公里换车.
公里换车.
若设行程为 公里(
公里( ),不换车的费用
),不换车的费用 (元),换车的费用
(元),换车的费用 (元),
(元),
则 ;
; .
.
请你帮忙计算一下,行程超过多少公里后换车会就会节约费用.
已知,如图,在菱形 中, 为边 的中点, 与对角线 交于点 ,过 作 于点 .
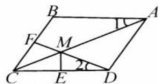
(1)若 ,求 的长;
(2)求证: .
现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.

已知 ,判定以 为边的四边形的形状.
下面有四个命题:
(1)一组对边相等且一组对角相等的四边形是平行四边形.
(2)一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形.
(3)一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形是平行四边形.
(4)一组对角相等且这一组对角的顶点所连接的对角线被另一条对角线平分的四边形是平行四边形.
上述命题是否正确?正确的请证明,错误的请举出反例.
如图,在 中, 是 的中点, 于点 ,求证: .
