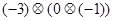现有一张矩形纸片 (如图)。其中 ,点 是 的中点,将纸片沿直线 折叠,点 落在四边形 内,记为点 ,求线段 的长.

阅读理解题(本题共14分)
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C(,),B→C(,),C→(+2,);
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出P的位置。
(4)请你为这只甲壳虫设计一种从A处去往E处的路线。
观察下列各式。 ,
, ,
, ,
,
…… …
(1)猜想填空: ( )2
( )2 ( )2
( )2
(2)求 的值
的值
阅读下题的计算方法。
计算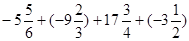 。
。
解:原式=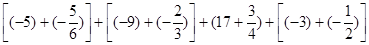
= 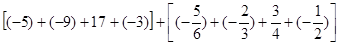
=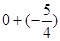
=
上面这种解题方法叫做拆项法,按此方法计算: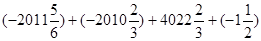
洋洋有4张卡片写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,如何抽取?最大值是多少?(2分)
(2)从中取出2张卡片,使这2张卡片上数字组成一个最大的数,如何抽取?最大的数是多少?
(3)将这4张卡片上的数字用学过的运算方法,使结果为24.写出运算式子(一种即可).
定义新运算: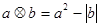 ,如
,如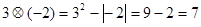 ,计算下列各式。
,计算下列各式。
(1)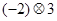 (2)
(2)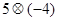 (3)
(3)