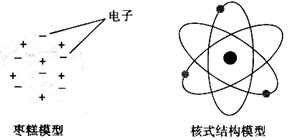
人们在研究原子结构时提出过许多模型，其中比较有名的是枣糕模型和核式结构模型，它们的模型示意图如图所示。下列说法中正确的是（ ）
A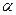． 粒子散射实验与枣糕模型和核式结构模型的建立无关 |
| B．科学家通过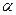粒子散射实验否定了枣糕模型，建立了核式结构模型 |
| C．科学家通过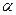粒子散射实验否定了核式结构模型，建立了枣糕模型 |
| D．科学家通过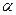粒子散射实验否定了枣糕模型和核式结构模型，建立了波尔的原子模型 |
从氢气放电管可以获得氢原子光谱。1885年瑞士中学教师巴尔末对当时已发现的在可见光区的谱线做了分析，发现这些谱线的波长可以用一个公式表示。如果采用波长
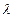的倒数，这个公式可写作：
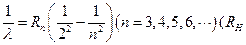为常数）
自巴尔末系发现后，人们又在紫外区和红外区发现了一些新的谱线，这些谱线也可以用类似巴尔末的简单公式来表示，例如赖曼系公式：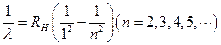
（RH为常数）
1913年丹麦物理学家玻尔提出了著名的原子结构和氢光谱理论。上述两个公式中的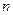
在波尔理论中被称为量子数。玻尔氢原子理论的能级图如图所示。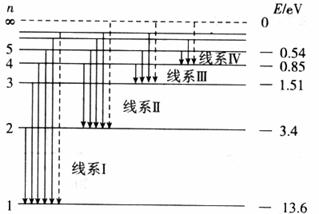
阅读了上面的资料后，你认为巴尔末系是氢原子能级图中的（ ）
| A．线系I | B．线系II | C．线系III | D．线系IV |
在光滑水平面上有一个静止的质量为M的木块，一颗质量为m的子弹以初速度v0水平射入木块而没有穿出，子弹射入木块的最大深度为d。设子弹射入木块的过程中木块运动的位移为s，子弹所受阻力恒定。试证明：s < d
一宇航员站在某质量分布均匀的星球表面上沿竖直方向以初速度v0抛出一个小球，测得小球经时间t落回抛出点，已知该星球半径为R，万有引力常量为G，求：该星球的密度．
如图所示，半径R＝0.4 m的光滑半圆轨道与粗糙的水平面相切于A点，质量为m＝1 kg的小物体(可视为质点)在水平拉力F的作用下，从静止开始由C点运动到A点，物体从A点进入半圆轨道的同时撤去外力F，物体沿半圆轨道通过最高点B后做平抛运动，正好落在C点，已知xAC＝2 m，F＝15 N，g取10 m/s2，试求：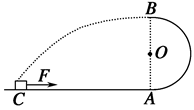
(1)物体在B点时的速度大小以及此时物体对轨道的弹力大小；
(2)物体从C到A的过程中，克服摩擦力做的功．
如图所示，轻杆长为L，球的质量为m，杆连球在竖直平面内绕轴O自由转动，已知在最高点处，杆对球的支持力大小为F=mg/2，
求：⑴小球在最高点的瞬时速度大小。
⑵小球到达最低点的动能。
将小球以6m/s的速度水平抛出去，它落地时的速度为10m/s，（g=10m/s2）求：
（1）小球运动的水平位移s；
（2）小球在空中下落的高度h。
低速载货汽车质量为5.0×103kg，其发动机的额定功率为3.75×104W，汽车在平直道路上从静止开始启动，开始一段时间内，以1 m／s2的加速度做匀加速直线运动，最终达到的最大速度为15m／s，假设它运动中所受阻力大小恒定，求：
(1)汽车运动中所受的阻力；
(2)汽车匀加速运动的时间。