如图所示，某滑道由AB、BC、CD三段轨道组成，轨道交接处均由很小的圆弧平滑连接（不考虑能量损失），其中轨道AB段是光滑的，水平轨道BC的长度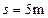
，轨道CD足够长且倾角
，A点离轨道BC的高度为
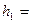4.30m。现让质量为m的小滑块自A点由静止释放，已知小滑块与轨道BC、CD间的动摩擦因数都为μ=0.5，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8。试求：
小滑块第一次到达C点时的速度大小
小滑块第一次和第二次经过C点的时间间隔
小滑块最终静止的位置距B点的距离
如图所示，一个半径为R的
透明圆柱体放置在水平面上，一束蓝光从A点沿水平方向射入圆柱体后经B点射出，最后射到水平面上的C点。已知OA＝
，该圆柱体对蓝光的折射率为
，则：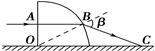
①它从圆柱面射出时的出射角β为多大？
②若换用一束红光同样从A点射向该圆柱体，则它从圆柱体射出后在水平面上形成的光点在C点的哪侧？
如图所示，一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体，活塞横截面积为S，气体最初的体积为V0，气体最初的压强为p0/2，汽缸内壁光滑且缸壁是导热的。开始活塞被固定，打开固定螺栓K，活塞下落，经过足够长时间后，活塞停在B点，设周围环境温度保持不变，已知大气压强为p0，重力加速度为g。若一定质量理想气体的内能仅由温度决定，求：
①活塞停在B点时缸内封闭气体的体积V；
②整个过程中通过缸壁传递的热量Q。
如图所示，在xOy平面中第一象限内有一点P(4，3)，OP所在直线下方有垂直于纸面向里的匀强磁场，OP上方有平行于OP向上的匀强电场，电场强度E＝100V/m。一质量m＝1×10－6kg，电荷量q＝2×10－3C带正电的粒子，从坐标原点O以初速度v＝1×103m/s垂直于磁场方向射入磁场，经过P点时速度方向与OP垂直并进入电场，在经过电场中的M点(图中未标出)时的动能为P点时动能的2倍，不计粒子重力。求：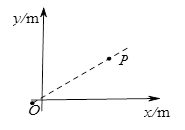
(1)磁感应强度的大小；
(2)O、M两点间的电势差；
(3)M点的坐标及粒子从O运动到M点的时间。
如图甲所示，“
”形木块放在光滑水平地面上，木块水平表面AB粗糙，光滑表面BC与水平面夹角为θ＝37°。木块右侧与竖直墙壁之间连接着一个力传感器，当力传感器受压时，其示数为正值；当力传感器被拉时，其示数为负值。一个可视为质点的滑块从C点由静止开始下滑，运动过程中，传感器记录到的力和时间的关系如图乙所示。已知sin37°＝0.6，cos37°＝0.8，g取10m/s2，求：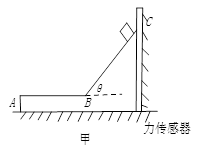
(1)斜面BC的长度；
(2)滑块的质量；
(3)运动过程中滑块克服摩擦力做的功。
在光滑水平面上有质量均为lkg，半径均为5cm的A、B两个小球.如图所示，小球.A从很远处以水平速度v0=2m/s向右正对B球运动,从某时刻两小球间开始有F=2N的恒定引力作用。在经过一段时间后，两球间距缩小4m，从此时刻起，两球间开始有F'=2N的恒定斥力作用。
(1)两球从开始有引力作用到开始有斥力作用经历时间为多少？
(2)为了使两球不相碰，开始有斥力时两球球心间距离应满足什么条件？