(本小题满分14分)求圆心在直线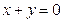 上,且过两圆
上,且过两圆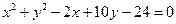 ,
,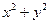
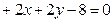 交点的圆的方程。
交点的圆的方程。
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
( ).
).
(1)求 的值;
的值;
(2)求 在
在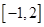 上的最大值;
上的最大值;
(3)当 时,
时, 对所有的
对所有的 及
及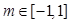 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
① ;
;
② ;
;
③ ;
;
④ ;
;
⑤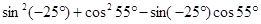 .
.
(1) 请根据(2)式求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为一个三角恒等式,并证明你的结论.
已知函数 .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)将函数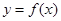 的图像向左平移
的图像向左平移 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数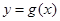 的图像,求
的图像,求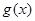 在
在 上的值域.
上的值域.
(1)已知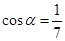 ,
,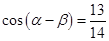 ,且
,且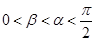 ,求
,求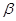 的值;
的值;
(2)已知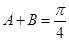 ,求证:
,求证: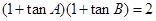 .
.
已知 为第三象限角,
为第三象限角,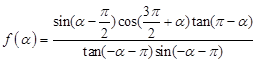 .
.
(1)化简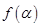 ;
;
(2)若 ,求
,求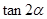 的值.
的值.