(本小题满分12分)已知f (x)=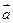 ·
· -1,其中向量
-1,其中向量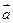 =(
=(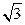 sin2x,cosx),
sin2x,cosx), =(1,2cosx)(x∈R)
=(1,2cosx)(x∈R)
(Ⅰ)求f (x)的单调递减区间;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,f (A)=2,a= ,b=
,b=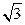 ,
,
求边长c的值。
在数列 中,
中, .
.
(1)求数列 的通项;
的通项;
(2)若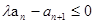 对任意的正整数
对任意的正整数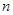 恒成立,求实数
恒成立,求实数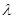 的取值范围.
的取值范围.
已知函数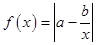 ,
,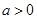 ,
,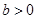 ,
,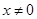 ,且满足:函数
,且满足:函数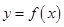 的图像与直线
的图像与直线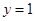 有且只有一个交点.
有且只有一个交点.
(1).求实数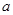 的值;
的值;
(2).若关于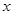 的不等式
的不等式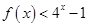 的解集为
的解集为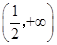 ,求实数
,求实数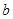 的值;
的值;
(3).在(2)成立的条件下,是否存在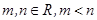 ,使得
,使得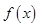 的定义域和值域均为
的定义域和值域均为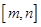 ,若存在,求出
,若存在,求出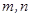 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
函数 的一段图象如图5所示:将
的一段图象如图5所示:将 的图像向右平移
的图像向右平移 个单位,可得到函数
个单位,可得到函数 的图象,且图像关于原点对称,
的图象,且图像关于原点对称,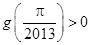 .
.
(1).求 的值;
的值;
(2).求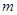 的最小值,并写出
的最小值,并写出 的表达式;
的表达式;
(3).若关于 的函数
的函数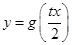 在区间
在区间 上最小值为
上最小值为 ,求实数
,求实数 的取值范围.
的取值范围.
如图所示,已知 是半径为1,圆心角为
是半径为1,圆心角为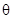 的扇形,
的扇形,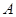 是扇形弧
是扇形弧 上的动点,
上的动点, ,
, 与
与 交于点
交于点 ,
,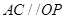 ,
, 与
与 交于点
交于点 .记
.记 .
.
(1).若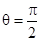 ,如图3,当角
,如图3,当角 取何值时,能使矩形
取何值时,能使矩形 的面积最大;
的面积最大;
(2).若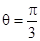 ,如图4,当角
,如图4,当角 取何值时,能使平行四边形
取何值时,能使平行四边形 的面积最大.并求出最大面积.
的面积最大.并求出最大面积.
已知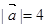 ,
, ,且
,且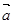 与
与 夹角为
夹角为 ,求
,求
(1). ;
;
(2).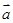 与
与 的夹角.
的夹角.