在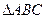 中,已知
中,已知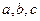 分别
分别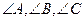 所对的边,
所对的边,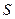 为
为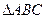 的面积,若
的面积,若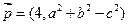 ,
, 满足
满足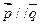 ,则
,则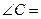
在平面直角坐标系内,设 、
、 为不同的两点,直线
为不同的两点,直线 的方程为
的方程为 , 设
, 设 有下列四个说法:
有下列四个说法:
①存在实数 ,使点
,使点 在直线
在直线 上;
上;
②若 ,则过
,则过 、
、 两点的直线与直线
两点的直线与直线 平行;
平行;
③若 ,则直线
,则直线 经过线段
经过线段 的中点;
的中点;
④若 ,则点
,则点 、
、 在直线
在直线 的同侧,且直线
的同侧,且直线 与线段
与线段 的延长线相交
的延长线相交
上述说法中,所有正确说法的序号是
在棱长为1的正方体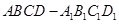 中,点
中,点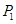 ,
,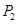 分别是线段
分别是线段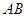 ,
, (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段 平行于平面
平行于平面 ,则四面体
,则四面体 的体积的最大值是_______
的体积的最大值是_______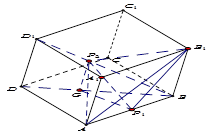
如图,二面角 的大小是60°,线段
的大小是60°,线段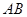 在平面EFGH上,
在平面EFGH上,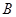 在EF上,
在EF上,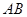 与EF所成的角为30°,则
与EF所成的角为30°,则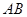 与平面
与平面 所成的角的正弦值是__________.
所成的角的正弦值是__________.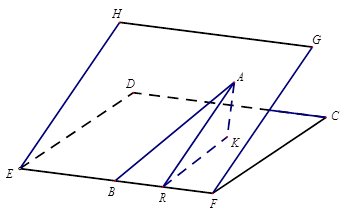
一个底面为正三角形,侧棱与底面垂直的棱柱,其三视图如图所示,则这个棱柱的体积为______.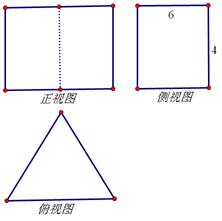
直线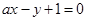 恒经过定点
恒经过定点 ,则
,则 点的坐标为______
点的坐标为______