(本小题满分14分)
已知点 、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 轴于点
轴于点 和点
和点 ,
,
(Ⅰ)用 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;
(Ⅱ)某同学发现,当曲线C的方程为: 时,
时, 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,  的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
(12分) 某制造商发现饮料瓶大小对饮料公司的利润有影响,于是该公司设计下面问题,问瓶子的半径多大时,能够使每瓶的饮料利润最大?瓶子的半径多大时,能使饮料的利润最小?
问题:若饮料瓶是球形瓶装, 球形瓶子的制造成本是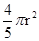 分,其中r(单位:cm)是瓶子的半径.已知每出售1ml的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为5cm.
分,其中r(单位:cm)是瓶子的半径.已知每出售1ml的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为5cm.
(12分)如图,矩形ABCD中,E是BC中点,DF⊥AE交AE延长线于F,AB="a" ,BC=b,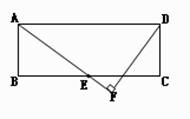
求证:DF=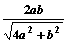
(12分)已知A={x|x2-3x-10≤0},B={x|m+1≤x≤2m-1},若A∪B=A,求m的取值范围。
(10分) 已知函数 在区间
在区间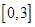 上有最小值-2,求实数a 的值
上有最小值-2,求实数a 的值
已知数列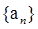 满足:
满足: ,
,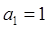 ,
, 为公差为4等差数列.数列
为公差为4等差数列.数列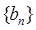 的前n项和为
的前n项和为 ,且满足
,且满足 .
.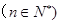
①求数列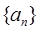 的通项公式
的通项公式 ;
;
②试确定 的值,使得数列
的值,使得数列 是等差数列;
是等差数列;
③设数列 满足:
满足:
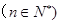 ,若在
,若在 与
与 之间插
之间插
入n个数,使得这 个数组成一个公差为
个数组成一个公差为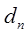 的等差数列.
的等差数列.
求证: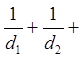 ……
…… 。
。