如右图,利用网格线作图:(本题6分)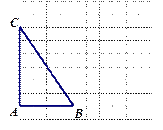
⑴画出将△ABC绕着点B顺时针旋转90°
后的△A′BC′;
⑵在BC上找一点P,使点P到AB和AC
的距离相等;
⑶在射线AP上找一点Q,使QB=QC.
如图,在平面直角坐标系中,已知点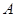 坐标为(2,4),直线
坐标为(2,4),直线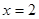 与
与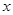 轴相交于点
轴相交于点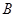 ,连结
,连结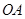 ,抛物线
,抛物线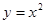 从点
从点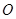 沿
沿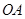 方向平移,与直线
方向平移,与直线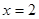 交于点
交于点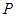 ,顶点
,顶点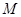 到
到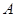 点时停止移动.
点时停止移动.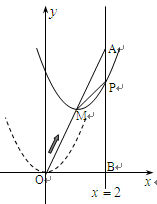
(1)求线段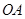 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点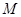 的横坐标为
的横坐标为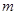 ,当
,当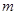 为何值时,线段
为何值时,线段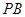 最短;
最短;
(3)当线段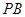 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点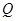 ,使△
,使△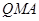 的面积与△
的面积与△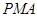 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点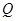 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
如图所示,现有一张边长为6的正方形纸片 ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP.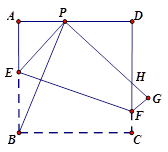
(1)求证:∠APB=∠BPH;
(2)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
根据对徐州市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数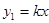 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数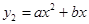 的图象如图②所示.
的图象如图②所示.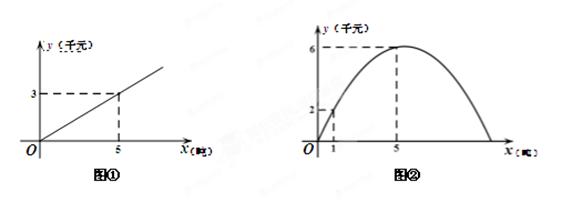
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时 获得的销售利润之和最大,最大利润是多少?
如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为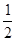 (即tan∠PAB=
(即tan∠PAB=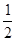 ,其中PB⊥AB ),且O、A、B在同一条直线上.
,其中PB⊥AB ),且O、A、B在同一条直线上.
(1)求此高层建筑的高度OC.(结果保留根号形式.);
(2)求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留根号形式.)
如图,⊙O的半径为l,等腰直角三角形ABC的顶点B的坐标为(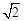 ,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.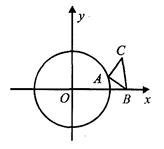
(1)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.