（本小题满分12分）
如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=EF=9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A 顺时针旋转，当DF边与AB边重合时，旋转中止。不考虑旋转开始和结束时重合的情况，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H点，如图（2）。
（1）问：始终与△AGC相似的三角形有 及 ；
（2）设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）；
（3）问：当x为何值时，△AGH是等腰三角形？
如图，在梯形ABCD中，已知AD∥BC， AB＝CD，延长线段CB到E，使BE＝AD，连接AE、AC．
（1）求证：△ABE≌△CDA；
（2）若∠DAC＝40°，求∠EAC的度数．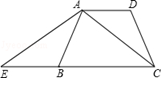
（1）解方程：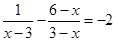
（2）求不等式组
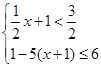的解集
（1）计算：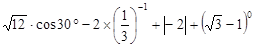
（2）化简：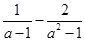
如图所示，已知点D为等腰直角△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝CA．
（1）求证：DE平分∠BDC；
（2）若点M在DE上，且DC=DM，求证： ME=BD．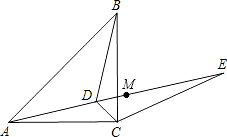
(10分)晓丽的家住在D处，每天她要送女儿到正东方向，距离家2500米外的幼儿园B处，然后沿原路返回到离家正西1500米C处上班，晓丽的工作单位的正北方向上有一家超市A.恰好晓丽家所在点D在公路AB、AC夹角的平分线上，你能求出晓丽的工作单位距离超市A有多远吗？