已知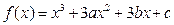
在
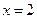处有极值，其图象在
处的切线与直线
平行。（1）求函数的单调区间；
（2）若
时，
恒成立，求实数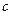
的取值范围。
以下是某地搜集到的新房屋的销售价格
（万元）和房屋的面积
（
）的数据 ，若由资料可知对呈线性相关关系。
试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为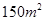
时的销售价格.
参考公式：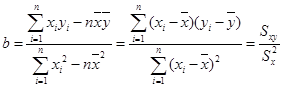
设数列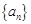
的前
项和为
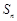，且满足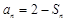
．
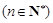（1）求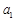
，
，
，
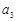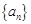的值并写出其通项公式；（2）证明数列是等比数列．
已知
．
（1）若曲线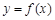
在
处的切线与直线
平行，求a的值；
（2）当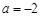
时，求
的单调区间．
如图，椭圆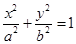
上的点M与椭圆右焦点
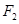的连线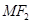
与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．
（1）求椭圆的离心率；
（2）F1是椭圆的左焦点，C是椭圆上的任一点，证明：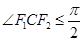
；
（3）过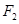且与AB垂直的直线交椭圆于P、Q，若
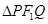的面积是20
，求此时椭圆的方程．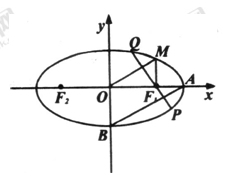
设函数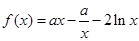
.
（1）若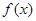
在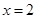
时有极值，求实数
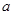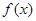的值和的极大值；
（2）若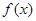在定义域上是增函数,求实数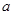的取值范围．