平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点(与F、G不重合)，PQ∥y轴与抛物线交于点Q。
求经过B、E、C三点的抛物线的解析式；
判断⊿BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标
若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由。
某初级中学准备随机选出七、八、九三个年级各1名学生担任领操员．现已知这三个年级分别选送一男、一女共6名学生为备选人.（1）请你利用树状图或表格列出所有可能的选法；
（2）求选出“两男一女”三名领操员的概率．
某区为了解全区2800名九年级学生英语口语考试成绩的情况，从中随机抽取了部分学生的成绩（满分24分，得分均为整数），制成下表：
| 分数段（x分） |
x≤16 |
17≤x≤18 |
19≤x≤20 |
21≤x≤22 |
23≤x≤24 |
| 人数 |
10 |
15 |
35 |
112 |
128 |
（1）填空：
①本次抽样调查共抽取了 ▲名学生；
②学生成绩的中位数落在▲分数段；
③若用扇形统计图表示统计结果，则分数段为x≤16的人数所对应扇形的圆心角为 ▲°；（2）如果将21分以上（含21分）定为优秀，请估计该区九年级考生成绩为优秀的人数．
如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，AE∥BC, DE∥AB.
证明：（1）AE=DC；（2）四边形ADCE为矩形．
先化简，再求值：
，其中a＝－2，b＝
．
如图，抛物线y=ax2+bx+c经过点A（
0，4）、B（2，4），它的最高点纵坐标为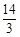
，点P是第一象限抛物线上一点且PA=PO，过点P的直线分别交射线AB、x正半轴于C、D．设AC=m，OD=n．
（1）求此抛物线的解析式；
（2）求点P的坐标及n关于m的函数关系式；
（3）连结OC交AP于点E，如果以A、C、E为顶点的三角形与△ODP相似，求m的值．