设椭圆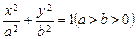 的左,右两个焦点分别为
的左,右两个焦点分别为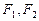 ,短轴的上端点为
,短轴的上端点为 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且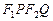 为正方形。
为正方形。
(1)求椭圆的离心率;
(2)若过点 作此正方形的外接圆的切线在
作此正方形的外接圆的切线在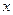 轴上的一个截距为
轴上的一个截距为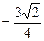 ,求此椭圆方程。
,求此椭圆方程。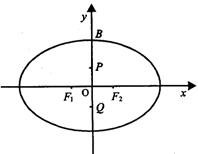
已知函数f(x)=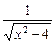 (x<-2).
(x<-2).
(1)求f(x)的反函数f--1(x);
(2)设a1=1, =-f--1(an)(n∈N*),求an;
=-f--1(an)(n∈N*),求an;
(3)设Sn=a12+a22+…+an2,bn=Sn+1-Sn是否存在最小正整数m,使得对任意n∈N*,有bn<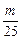 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.
设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.
(1)求证: f(x)为奇函数;
(2)在区间[-9,9]上,求f(x)的最值.
甲、乙两地相距S千米,汽车从甲地匀速驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的平方成正比,比例系数为b,固定部分为a元
(1)把全程运输成本y(元)表示为v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
设f(x)是定义在R上的偶函数,其图像关于直线x=1对称,对任意x1、x2∈[0, ],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
(1)求f( )、f(
)、f(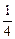 );
);
(2)证明f(x)是周期函数;
(3)记an=f(2n+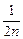 ),求
),求
若a>0,b>0,a3+b3=2,求证:a+b≤2,ab≤1。