已知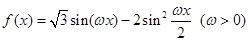 的最小正周期为
的最小正周期为 .
.
(Ⅰ)当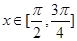 时,求函数
时,求函数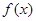 的最小值;
的最小值;
(Ⅱ)在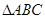 ,若
,若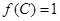 ,且
,且 ,求
,求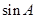 的值.
的值.
已知函数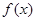 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当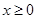 时,
时,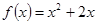 .
.
(1)写出函数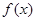 在
在 的解析式;
的解析式;
(2)若函数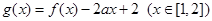 ,求函数
,求函数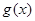 的最小值.
的最小值.
已知正方体 中,面
中,面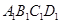 中心为
中心为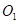 .
.
(1)求证: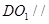 面
面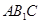 ;
;
(2)求异面直线 与
与 所成角.
所成角.
风景秀美的京娘湖畔有四棵高大的银杏树,记做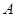 、
、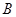 、
、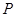 、
、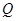 ,欲测量
,欲测量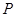 、
、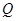 两棵树和
两棵树和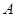 、
、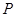 两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得
两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得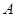 、
、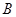 两点间的距离为
两点间的距离为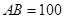 米,如图,同时也能测量出
米,如图,同时也能测量出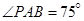 ,
,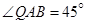 ,
,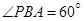 ,
,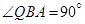 ,则
,则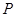 、
、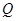 两棵树和
两棵树和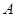 、
、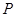 两棵树之间的距离各为多少?
两棵树之间的距离各为多少?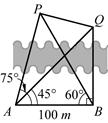
某种产品的广告费支出 与销售额
与销售额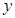 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
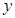 |
30 |
40 |
60 |
50 |
70 |
(1)求回归直线方程。
(2)试预测广告费支出为10百万元时,销售额多大?