(经典题)为了庆祝中国足球队首次进入世界杯赛,曙光体育器材厂赠送一批足球给希望中学足球队.若足球队每人领一个少6个球,每两人领一个则余6个球,问这批足球共多少个?小明领到足球后十分高兴,就仔细地研究起足球上的黑白球(如图),结果发现,黑块呈五边形,白色呈六边形,黑白相间在球体上,黑块共12块,问白块有多少块?
计算:
(1)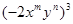 ·
·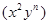 ·
·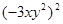
(2)
求下列各式中的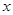 .
.
(1)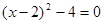
(2)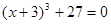
附加题
把几个数用大括号围起来,各数中间用逗号隔开,如:{1,2,-3}、
{−2,7, 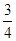 ,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
,19},数学上称作集合,其中的数称作集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称作“好集合” 如{5,0}就是一个好集合.
(1)请你判断集合{1,2},{-2,1,2.5,4,7}是不是“好集合”?
(2)请你再写出两个“好集合”(不得与上面出现过的集合重复).
(3)写出所有“好集合”中,元素个数最少的集合.
如图,已知线段a,b,且a>b,用直尺和圆规作一条线段,
使它等于2a-b.(保留作图痕迹)
把下面的有理数在数轴上表示出来,然后把它们用“<”连接起来。
3,-1.5, ,0,-4.
,0,-4.