已知椭圆E: (
(


 0)过点(0,
0)过点(0, ),其左焦点
),其左焦点 与点P(1,
与点P(1, )的连线与圆
)的连线与圆 相切。
相切。
(1)求椭圆E的方程;
(2)设Q为椭圆E上的一个动点,试判断以 为直径的圆与圆
为直径的圆与圆 的位置关系,并证明
的位置关系,并证明
(本小题满分8分)一个盒子中装有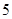 张卡片,每张卡片上编有一个数字,分别是 1,2,3,4,5现从盒子中随机抽取卡片
张卡片,每张卡片上编有一个数字,分别是 1,2,3,4,5现从盒子中随机抽取卡片
(1)若一次抽取 张卡片,求所抽取的三张卡片的数字之和大于
张卡片,求所抽取的三张卡片的数字之和大于 的概率
的概率
(2)若从编号为1、2、3、4的卡片中抽取,第一次抽一张卡片,放回后再抽取一张卡片,求两次抽取至少一次抽到数字 的卡片的概率.
的卡片的概率.
(本小题满分14分)已知函数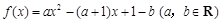 .
.
(Ⅰ)若 ,关于
,关于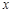 的不等式
的不等式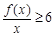 在区间
在区间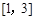 上恒成立,求
上恒成立,求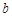 的取值范围;
的取值范围;
(Ⅱ)若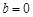 ,解关于
,解关于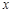 的不等式
的不等式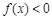 ;
;
(Ⅲ)若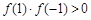 ,且
,且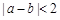 ,求
,求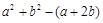 的取值范围.
的取值范围.
(本小题满分13分)已知点 ,点
,点 ,直线l:
,直线l: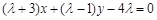 (其中
(其中 ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若直线l与线段AB有公共点,求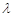 的取值范围;
的取值范围;
(Ⅲ)若分别过A,B且斜率为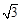 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为 ,求直线
,求直线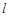 的方程.
的方程.
(本小题满分12分)在数列 中,
中, ,又
,又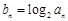 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)设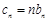 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)在△ABC中,角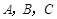 对边分别为
对边分别为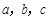 .设向量
.设向量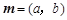 ,
, ,
,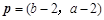 .
.
(Ⅰ)若m∥n,求证:△ABC为等腰三角形;
(Ⅱ)已知c=2, ,若m⊥p,求△ABC的面积S.
,若m⊥p,求△ABC的面积S.