(本小题满分13分)已知点 ,点
,点 ,直线l:
,直线l: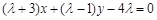 (其中
(其中 ).
).
(Ⅰ)求直线l所经过的定点P的坐标;
(Ⅱ)若直线l与线段AB有公共点,求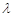 的取值范围;
的取值范围;
(Ⅲ)若分别过A,B且斜率为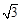 的两条平行直线截直线l所得线段的长为
的两条平行直线截直线l所得线段的长为 ,求直线
,求直线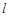 的方程.
的方程.
(本小题满分12分)
已知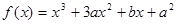 在
在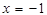 时有极值0.
时有极值0.
(1)求常数a、b的值;
(2)求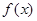 的单调区间.
的单调区间.
(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,平面PAD⊥平面ABCD,E、F分别为PC和BD的中点.
(1)证明:EF∥平面PAD;
(2)证明:平面PDC⊥平面PAD.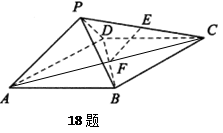
(本小题满分10分)
已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为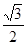 ,且经过点
,且经过点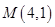 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(1)求椭圆的方程;
(2)求 的取值范围。
的取值范围。
(本小题满分12分)设函数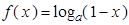 ,
, (
( 且
且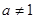 )。
)。
(1)设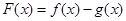 ,判断
,判断 的奇偶性并证明;
的奇偶性并证明;
(2)若关于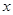 的方程
的方程 有两个不等实根,求实数
有两个不等实根,求实数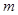 的范围;
的范围;
(3)若 且在
且在 时,
时,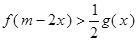 恒成立,求实数
恒成立,求实数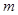 的范围。
的范围。
(本题满分12分) 设 是定义在
是定义在 上的增函数,令
上的增函数,令
(1)求证 时定值;
时定值;
(2)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若 ,求证
,求证 。
。