如图,已知椭圆 的上顶点为
的上顶点为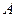 ,右焦点为
,右焦点为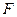 ,直线
,直线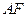 与圆
与圆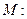
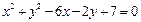 相切.
相切.
(Ⅰ)求椭圆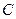 的方程;
的方程;
(Ⅱ)若不过点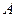 的动直线
的动直线 与椭圆
与椭圆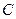 相交于
相交于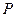 、
、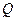 两点,且
两点,且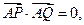 求证:直线
求证:直线 过定点,并求出该定点
过定点,并求出该定点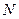 的坐标
的坐标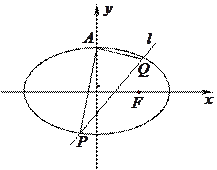
已知向量=(1+tanx,1-tanx),=(sin(x-),sin(x+)).
(1)求证:⊥;(2)若x∈[-,],求||的取值范围.
(本题满分共13分)已知正项数列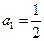 ,函数
,函数 。(1)若正项数列
。(1)若正项数列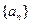 满足
满足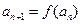 (
(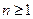 且
且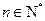 ),试求出
),试求出 由此归纳出通项
由此归纳出通项 ,并证明之;(2)若正项数列
,并证明之;(2)若正项数列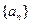 满足
满足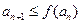 (
(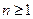 且
且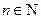 ),数列
),数列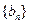 满足
满足 ,其和为
,其和为 ,求证
,求证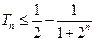 。
。
(本题满分共13分)已知函数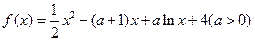 (1)求函数
(1)求函数 的单调递减区间;(2)当
的单调递减区间;(2)当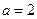 时,函数
时,函数 在
在 有零点,求
有零点,求 的最大值。
的最大值。
为了美化环境,构建两型社会,市城建局打算在广场上建造一个绚丽多彩的矩形花园,中间有三个完全一样的矩形花坛,每个花坛面积均为294平方米,花坛四周的过道均为2米,如图所示,设矩形花坛的长为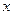 ,宽为
,宽为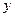 ,整个矩形花园面积为
,整个矩形花园面积为 。(1)试用
。(1)试用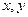 表示S;(2)为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,占地多少平米?
表示S;(2)为了节约用地,当矩形花坛的长为多少米时,新建矩形花园占地最少,占地多少平米?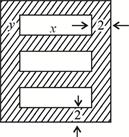
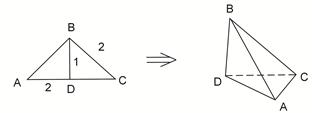
(本题满分共12分)如图,在 中,
中,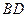 为
为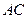 边上高,
边上高,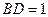 ,
,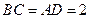 ,沿
,沿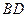 将
将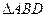 翻折,使得
翻折,使得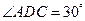 ,得到几何体
,得到几何体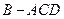 。(1)求证:
。(1)求证: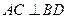 ;
;
(2)求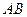 与平面
与平面 成角的正切值。
成角的正切值。