（本题10分）近几年后，实验中学准备搬迁新校舍，在迁入新校舍之前，同学们就学校学生如何到校问题进行了一次调查，并将调查结果制成了表格、条形图和扇形统计图，请你根据图表信息完成下列各题：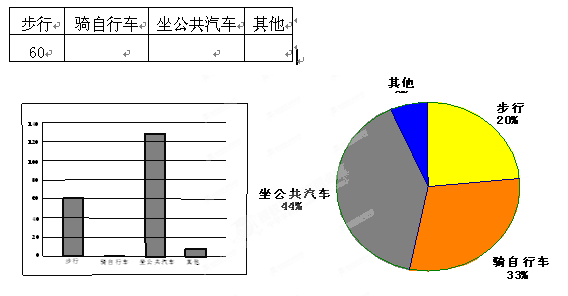
（1）此次共调查了多少位学生？
（2）请将表格填充完整；
（3）请将条形统计图补充完整.
(本题8分)如图，两个同心圆，大圆的弦AB和AC分别切小圆于点D,E.
求证：DE∥BC
(本题8分)关于
的一元二次方程
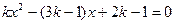,其根的判别式的值为1，求
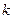的值及方程的根
.
(本题6分)如图，AD、BC是⊙O的两条弦，且AD=BC，
求证：AB=CD。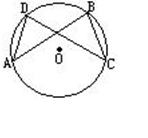
(本题8分)已知一元二次方程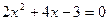
.
（1）不解方程，试说明该方程有两个不相等的实数根；
（2）设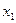
，
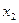是
此方程的两个根，求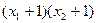
的值.
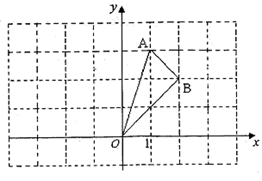
（本题6分）如图，在平面直角坐标系xOy中，△AOB三个顶点的坐标分别为
O（0，0），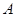
（1，3），
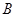（2，2），将△AOB绕点O逆时针旋转90°后，点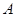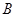， 分别落在点
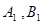处。
（1）在所给的平面直角坐标系xOy中画出旋转后的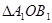
；
（2）求点B旋转到点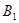
所经过的弧形路线的长.