抛物线
 交
交 轴于
轴于 、
、 两点,交
两点,交 轴于点
轴于点 ,顶点为
,顶点为 .
.
(1)写出抛物线的对称轴及
 、
、 两点的坐标(用含
两点的坐标(用含 的代数式表示)
的代数式表示)(2)连接
 并以
并以 为直径作⊙
为直径作⊙ ,当
,当 时,请判断⊙
时,请判断⊙ 是否经过点
是否经过点 ,并说明理由;
,并说明理由;(3)在(2)题的条件下,点
 是抛物线上任意一点,过
是抛物线上任意一点,过 作直线垂直于对称轴,垂足为
作直线垂直于对称轴,垂足为 . 那么是否存在这样的点
. 那么是否存在这样的点 ,使△
,使△ 与以
与以 、
、 、
、 为顶点的三角形相似?若存在,请求出点
为顶点的三角形相似?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知一元二次方程x2+ax+a-2=0.
(1)求证:不论a为何实数,此方程总有两个不相等的实数根;
(2)设a<0,当二次函数y=x2+ax+a-2的图象与x轴的两个交点的距离为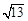 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为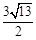 ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.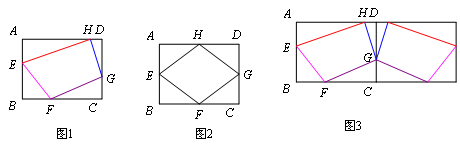
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=________.
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.
①请在图1中补全小贝同学翻折后的图形;
②m的取值范围是____________.
如图,已知 ,以
,以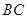 为直径,
为直径,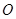 为圆心的半圆交
为圆心的半圆交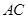 于点
于点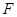 ,点
,点 为弧CF的中点,连接
为弧CF的中点,连接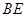 交
交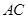 于点
于点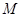 ,
,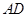 为△ABC的角平分线,且
为△ABC的角平分线,且 ,垂足为点
,垂足为点 .
.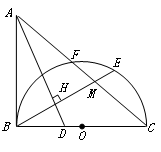
(1)求证: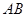 是半圆
是半圆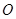 的切线;
的切线;
(2)若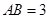 ,
,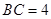 ,求
,求 的长.
的长.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.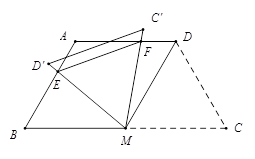
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单位应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需要化简)
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
▲ |
40 |
| 销售量(件) |
200 |
▲ |
▲ |
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?